Physics Numerical for class 9 motion & other chapters with answers & [PDF]
Last updated on December 12th, 2023 at 01:53 pm
This is an online guide on Physics Numerical for Class 9. It presents a super-set of Numerical Problems on Motion and other Chapters in Class 9 Science for CBSE, ICSE, & UPSC. The full set contains 101+ problems with solutions for most of the problems.
For faster loading of the page, we have broken down the series into multiple pages. The links are given at the end of this post for the next pages. You will get a PDF download link as well on this page.
Numerical Problems from class 9 Motion (with solution)
The next set of numerical questions (set 1) covers questions from the Motion chapter (kinematics) of class 9 physics and these can be easily solved using motion equations (Suvat equations).
Formulas Used
v=u + at
s= ut + (1/2)at2
s = [(u+v)/2]. t
v2=u2 + 2as
1) A speedboat has an acceleration of 2 m/s2. What would the final velocity of the speedboat be after 5 seconds if the initial velocity of the speedboat is 4 m/s?
Solution:
a = 2 m/s2
u = 4 m/s
t = 5 s
final velocity = v
v = u + at = 4 + 2×5 = 14 m/s
2) A vehicle has an acceleration of 5 m/s2. What would the final velocity of the vehicle be after 10 seconds if the initial velocity of the vehicle is 20 m/s? What is the displacement of the vehicle during the 10 s time interval?
Solution:
a = 5 m/s2
u = 20 m/s
t = 10 s
final velocity = v
v = u + at = 20 + 5×10 = 70 m/s
final velocity = 70 m/s
Displacement during the 10 s time interval = s
s = ut + (1/2)at2
=> s = 20×10 + (½)x5x102
=> s= 200 + 250 = 450 m
Displacement during the 10 s time interval = 450 m
3) A child on a toboggan starts from rest and accelerates down a snow-covered hill at 0.8 m/s2. How long does it take the child to reach the bottom of the hill if it is 25.0 m away?
Solution: initial velocity u = 0
acceleration a = 0.8 m/s2
distance = s = 25 m
time taken t = ?
s= ut + (1/2)at2
As here, u = 0, so we can write:
s= (1/2)at2
=> t2 =(2 s /a ) = (2×25)/0.8 = 62.5
time t = 7.9 sec
4. A car accelerates uniformly from a velocity of 21.8 m/s to a velocity of 27.6 m/s. The car travels 36.5 m during this acceleration.
a) What was the acceleration of the car?
b) Determine the time interval over which this acceleration occurred.
Solution:
a) final velocity v = 27.6 m/s
initial velocity u = 21.8 m/s
distance traveled s=36.5 m
We will use this equation: v2 = u2 + 2as
a = ( v2 – u2) /(2s) = (27.62 – 21.82)/(2×36.5) = 3.92 m/s2
Acceleration = 3.92 m/s2
b) time interval over which this acceleration occurred = t
v = u + at
=> t = (v-u)/a = (27.6-21.8) / 3.92 = 1.48 seconds.
5. A motorcycle starts from rest and accelerates at +2.50 m/s2 for a distance of 150.0 m. It then slows down with an acceleration of –1.50 m/s2 until the velocity is +10.0 m/s. Determine the total displacement of the motorcycle.
Solution:
First part:
displacement = s = 150 m
We need to find out the final velocity(v) of this accelerating part.
v2 = u2 + 2as
=> v2 = 0 + 2×2.5×150 = 750
=> v = 27.4 m/s
This velocity becomes the initial velocity of the second part of the journey.
Second part:
u = 27.4 m/s
a = -1.5 m/s2
v= 10 m/s
v2 = u2 + 2as
102 = 27.42 + 2.(-1.5).s
=> 100 = 750 – 3s
s= 650/3 = 216.7 m
Second part displacement = 216.7 m
Considering a straight-line journey without a change of direction,
total displacement = (150 + 216.7) m = 366.7 m
Physics Numericals Class 9 From Different Chapters
So let’s start with sets of Physics Numericals for Class 9 which contains Numerical problems & questions from various chapters of Class 9 physics with solutions & answers.
Problems based on Newton’s Second Law
Formulas Used
F = ma
m = F/a
a = F/m
F = (mv – mu)/t
1) A force of 1000 Newton is applied on a 25 kg mass for 5 seconds. What would be its velocity?
Solution:
F =1000 N
m=25kg
t= 5 sec
u=0
v=?
Acceleration = a = F/m = 1000/25 = 40 m/s2
v = u + at =0 + 40X5 = 200 m/s
2) A force is applied to a mass of 16 kg for 3 seconds. As the force is removed the mass moves 81 meters in 3 seconds. What was the value of the force applied?
Solution:
First 3 secs: Force is present, and in the next 3 secs Force is not there, so uniform velocity for the last 3 seconds is mentioned.
In the last 3 seconds, the mass travels with uniform velocity
(Where no force means there is no acceleration).
So the velocity in the next 3 secs:
V = 81/3 = 27 m/s
This velocity was attained in the first 3 seconds when the force was present.
So in the first 3 seconds, velocity changes from 0 to 27m/s.
Therefore the acceleration in the first 3 seconds caused by the force present = (27-0)/3 = 9 m/s².
So the force applied on the mass for first 3 secs= mass x acc = 16 x 9 = 144 N
3) A mass of 50 kg was moving with a velocity of 400 m/s. A force of 40000 N is applied to the mass and its velocity is reduced to 50 m/s after some time. What is the distance traveled by the mass during this period?
Solution:
Mass = 50 kg
u = 400 m/s
v= 50 m/s
F = 40000 N
t = unknown
Distance traveled in time t =?
Acceleration = a = F/m = 40000/50 = 800 m/s2
Again, acceleration a = change of velocity /t
or, t = change of velocity/a = 350/800 sec
Distance traveled: s = ut – (1/2)a t2
= 400 * (350/800) – (1/2) 800. (350/800)2
= 175 – 76.5 = 98.5 m
4) A ball of 150 g mass moves with 12 m/s and bounces back after hitting a wall with 20 m/s after a small duration of 0.01 seconds. What was the force applied to the ball when it hits the wall?
Solution:
Mass = 150 gram = 150/1000 kg = 0.15 kg
Change of velocity = 20 – (-12) = 32 m/s
T = 0.01 sec
Acceleration = change in velocity / time = 32/0.01 = 3200 m/s2
Force = mass X Acceleration = 0.15 X 3200 N= 480 N.
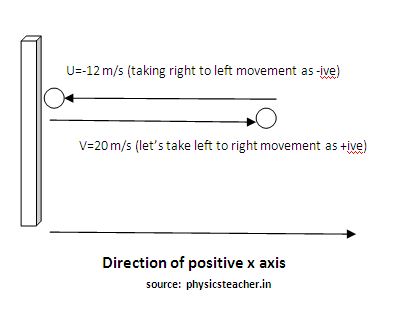
5) Momentum of an object changes from 100 kg m/s to 200 kg m/s in 2 seconds. What is the force applied to it?
Solution:
Note:
Force = ma = m(v-u)/t = (mv – mu)/t = change of momentum /time = rate of change of momentum
Force= change of momentum /time = (200-100)/2 = 100/2 = 50 N
6) A force of 200 N is applied to a body and its velocity changes from 5m/s to 10m/s in a second. What is the mass of the body?
Solution:
mass = force/acceleration
here acceleration =a = (10-5)/1 = 5 m/s2
so, mass = 200/5 kg = 40 kg
7) A mass of 1 kg is moving from east to west with a velocity of 10 m/s. A force is applied to it for 2 seconds and its velocity becomes 5 m/s. What is the value and direction of the force?
Solution:
Mass = 1kg
velocity = 10 m/s (east to west)
Because of the force, the velocity reduces to 5 m/s in 2 secs.
acceleration = change of vel/time=5/2 = 2.5 m/s2
Force = mass X acceleration= 1 X 2.5 = 2.5 N.
As the velocity reduces because of force, (negative acc i.e. retardation) hence the direction of the force would be opposite to the initial direction. So the direction of the force will be west to east.
Problems based on the Universal Law of Gravitation
Formulas Used
F = GMm/r2
8) If the distance between 2 objects is doubled then how will the gravitational force between them change?
Solution:
F1 = GMm/r2
F2 = GMm/(2r)2
= GMm/4r2
so F2/F1 = ¼ ,
so the final gravitational force will be ¼th of the initial gravitational force
9) If the distance between 2 objects is halved then how will the gravitational force between them change?
Solution:
F1 = GMm/r2
F2 = GMm/(r/2)2
=4 GMm/r2
so F2/F1 = 4/1
so the final gravitational force will be 4 times the initial gravitational force
10) If the masses of the 2 objects are doubled then how will the gravitational force between them change?
Solution:
F1 = GMm/r2
F2 = (G2M2m)/(r)2
=4 GMm/r2
so F2/F1 = 4/1
so the final gravitational force will be 4 times the initial gravitational force
Problems based on Force, Acceleration, and Motion
11) A force acts for 10 s on a stationary body of mass 100 kg after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate (i) the velocity acquired by the body, (ii) the acceleration produced by the force, and (iii) the magnitude of the force.
[ Solution: Q11 ]
12) A force acts for 0.1 sec on a body of mass 2 kg initially at rest. The force is then withdrawn and the body moves with a velocity of 2 m/s. Find the magnitude of the force.
Solution: solution Q12
13) A cricket ball of mass 100 g moving at a speed of 30 m/s is brought to rest by a player in 0.03 s. find the average force applied by the player.
Solution: solution Q13
14) A body of mass 500 g, initially at rest, is acted upon by a force that causes it to move a distance of 4 m in 2 sec. Calculate the force applied.
Solution: solution Q14
15) A force causes an acceleration of 10 m/s^2 in a body of mass 500 g. What acceleration would be caused by the same force in a body of mass 5 kg.
Solution: solution Q15
16) A bullet of mass 50 g moving with an initial velocity of 100 m/s, strikes a wooden block and comes to rest after penetrating a distance 2 cm in it.
Calculate:
(i) Initial momentum of the bullet (ii)final momentum of the bullet (iii) retardation caused by the wooden block, and (iv) resistive force exerted by the wooden block
Solution: solution Q16
Find another set of Physics Numerical for Class 9 Motion.
17) From the velocity-time graph, find out the distance traveled in each section A, B, C, and D. Also find the total distance traveled.
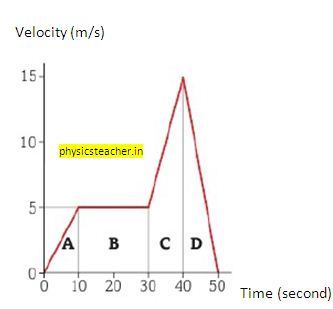
Solution: solution Q17
18) A car starts from rest and accelerates uniformly over a time of 7 seconds for a distance of 98 m. Determine the acceleration of the car.
Solution: solution Q18
19) A car traveling at 20 m/s skids to a stop in 3 s. Determine the skidding distance of the car (assume uniform acceleration).
Solution: solution Q19
20) An airplane accelerates down a runway at 4 m/s^2 for 30 s until it finally lifts off the ground. Determine the distance traveled before takeoff.
Solution: solution Q20
21) A feather is dropped on the moon from a height of 10 meters. The acceleration of gravity on the moon is one-sixth of that on the earth. Determine the time for the feather to fall to the surface of the moon.
Solution: solution Q 21
22) If a rocket-powered sled is accelerated to a speed of 400 m/s in 2 seconds, then what is the acceleration, and what is the distance that the sled travels?
Solution: solution Q22
23) An engineer is designing the runway for an airport. Of the planes that will use the airport, the lowest acceleration rate is likely to be 3 m/s2. The takeoff speed for this plane will be 65 m/s. Assuming this minimum acceleration, what is the minimum allowed length for the runway?
Solution: solution Q 23
24) Upton Chuck is riding the Giant Drop at Great America. If Upton free falls for 2.60 seconds, what will be his final velocity and how far will he fall?
Solution: solution Q 24
25) A bike accelerates uniformly from rest to a speed of 10 m/s over a distance of 30 m. Determine the acceleration of the bike.
Solution: solution Q25
26) A race car accelerates uniformly from 25 m/s to 50 m/s in 5 seconds. Determine the acceleration of the car and the distance traveled.
Solution: solution Q 26
27) A bullet leaves a rifle with a muzzle velocity of 600 m/s. While accelerating through the barrel of the rifle, the bullet moves a distance of 0.8 m. Determine the acceleration of the bullet (assume uniform acceleration).
Solution: solution Q 27
28) A bullet is moving at a speed of 350 m/s when it embeds into a lump of moist clay. The bullet penetrates for a distance of 0.05 m. Determine the acceleration of the bullet while moving into the clay. (Assume a uniform acceleration.)
Solution: solution Q 28
29) A plane has a takeoff speed of 100 m/s and requires 1500 m to reach that speed. Determine the acceleration of the plane and the time required to reach this speed.
Solution: solution Q29
30)A baseball is popped straight up into the air and has a hang-time of 6 s. Determine the height to which the ball rises before it reaches its peak. (Hint: the time to rise to the max height is one-half the total hang time.)
Solution: solution Q30
31) If a box is pushed horizontally on the floor with a force of 10 N and it moves 5 meters along the line of action of the force, then what is the work done by the Gravity or earth’s gravitational pull on that box?
Solution: solution Q31
32) A train is moving at a velocity of 25 ms-1. It is brought to rest by applying the brakes which produce uniform retardation of 0.5 ms-2.
Calculate
(i) the velocity of the train after 10 s
(ii) If the mass of the train is 20000 kg then calculate the force required to stop the train
Solution: solution Q32
33) A spring balance is used to find the weight of a body X on the surface of the moon. The mass of the body X is 2 kg and its weight is recorded as 3.4 N. The weight of another body Y recorded by the same balance is found to be 7.65 N. Calculate the mass of the body Y.
Solution: solution Q33
Gravitational force numerical
34) Calculate the force of gravitation between two objects of masses 50 kg and 120 kg respectively kept at a distance of 10 m from one another. (Gravitational constant, G = 6.7 × 10 -11 Nm^2/kg^2 )
Solution: solution Q34
35) What is the force of gravity on a body of mass 150 kg lying on the surface of the earth?
(Mass of earth = 6 × 10^24 kg; Radius of earth = 6.4 × 10^6 m; G = 6.7 × 10 -11 Nm^2/kg^2)
Solution: solution Q35
36) The mass of sun is 2 × 10^30 kg and the mass of earth is 6 × 10^24 kg. If the average distance between the sun and the earth is 1.5 × 10^8 km, calculate the force of gravitation between them.
Solution: solution Q36
Vertical Motion questions
The following set on physics numerical for class motion specifically covers vertical motion questions.
37) A piece of stone is thrown vertically upwards. It reaches the maximum height in 3 seconds. If the acceleration of the stone is 9.8 m/s^2 directed towards the ground, calculate the initial velocity of the stone with which it is thrown upwards.
Solution: solution Q37
38) A stone falls from a building and reaches the ground 2.5 seconds later. How high is the building? (g = 9.8 m/s^2)
Solution: solution Q38
39) A stone is dropped from a height of 20 m.(i) How long will it take to reach the ground? (ii) What will be its speed when it hits the ground? (g = 10 m/s^2)
Solution: solution Q39
40) A stone is thrown vertically upwards with a speed of 20 m/s. How high will it go before it begins to fall? (g = 9.8 m/s^2)
Solution: solution Q40
41) When a cricket ball is thrown vertically upwards, it reaches a maximum height of 5 meters. (a) What was the initial speed of the ball? (b) How much time is taken by the ball to reach the highest point? (g =10 m/ s^2)
Solution: solution Q41
Numerical questions on Mass, Weight & acceleration due to gravity (g)
42) A force of 20 N acts upon a body whose weight is 9.8 N. What is the mass of the body and how much is its acceleration? (g = 9.8 m/ s^2).
Solution: solution Q42
43) A stone resting on the ground has a gravitational force of 20 N acting on it. What is the weight of the stone? What is its mass? ( g = 10 m/s^2).
Solution: solution Q43
44)
(a) An object has a mass of 20 kg on Earth.
What will be its (i) mass, and (ii) weight, on the moon? (g on moon = 1.6 m/s^2).
(b) Calculate the acceleration due to gravity on the surface of a satellite having a mass of 7.4 × 10^22 kg and a radius of 1.74 × 10^6 m (G = 6.7 × 10 -11 Nm^2/kg^2).
Solution: solution Q44
45) The mass of a planet is 6 × 10^24 kg and its diameter is 12.8 × 10^3 km. If the value of the gravitational constant is 6.7 × 10 -11 Nm2/kg2, calculate the value of acceleration due to gravity on the surface of the planet.
Solution: solution Q45
46) The values of g at six distances A, B, C, D, E, and F from the surface of the earth are found to be 3.08 m/s^2, 9.23 m/s^2, 0.57 m/s^2, 7.34 m/s^2, 0.30 m/s^2 and 1.49 m/s^2, respectively.
(a) Arrange these values of g according to the increasing distances from the surface of the earth (keeping the value of g nearest to the surface of the earth first)
(b) If the value of distance F be 10000 km from the surface of the earth(hint: check if possible or not), state whether this distance is deep inside the earth or high up in the sky.
Give the reason for your answer of the place of observation
Solution: solution Q46
47) A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m/s^2 and speed of sound = 330 m/s, find (i) the depth of the water surface, and (ii) the time when the echo is heard after the pebble is dropped.
**[answer Hint: 2000 m ; 26.06 secs ]
Solution: solution Q47
48) A ball is thrown vertically upwards from the top of a tower with an initial velocity of 19·6 m/s. The ball reaches the ground after 5 s. Calculate: (i) the height of the tower, (ii) the velocity of ball on reaching the ground. Take g = 9·8 m/s^2
**[answer Hint: 24.5 m ; 29.4 m/s ]
Solution: solution Q48
We have 53 more numerical questions in this series for class 9 physics – these are listed on the next pages of this series. You will find the links to these pages below.



I find this collection of physics problems very useful. Our class teacher has also prescribed us to solve these problems. Thank you.
Many thanks for putting in the effort for students like me. I am solving these problems even for the competitive exams I will have soon.
You have a good amount of materials for physics problems. I found this site very helpful. One request: can you post chemistry problems as well?
Thanks for your comments and suggestion, Shilpa. We will certainly plan for it.
Hi Ayan, Good to know this. Best wishes.
Thanks Dip for your inspiring words.