Gravitation class 9 Numericals

Last updated on July 27th, 2023 at 10:07 am

Here we will solve a bunch of Gravitation Numericals for class 9. This is a set of numerical questions on the class 9 gravitation chapter. The solution is also provided after each question of this numerical set.

This solved question-answer set is appropriate for high school students of IGCSE, ICSE, CBSE, and State Boards, and is good for competitive exams as well.

Formulas Used

Formula of Gravitational force:   
F_G = (G.m1.m2)/r², where G is a constant which is known as Universal Gravitational Constant or Gravitational constant. This equation gives us the expression of the gravitational force.

Acceleration due to gravity: g= GM / R²
R = radius of the earth & M = Mass of the earth.

Gravitation class 9 Numericals [solved]

Question 1 ] Find the gravitational force of attraction between a body of unit mass and the Moon.
Mass of the moon = 7.4 x 10^22 kg
radius of the moon = 1.74 x 10^6 m
G = 6.67 x 10^(-11) N-m^2/kg^2

Solution:

2 ] What is the gravitational force between the Sun and the Earth?

(take, the mass of the Sun = 1.99 x 10^30 Kg.
mass of the Earth = 6 x 10^24 Kg
G = 6.67 x 10^(-11) N-m^2/kg^2
and distance between the Sun and the Earth=1.49 x 10^11 m)

Solution:

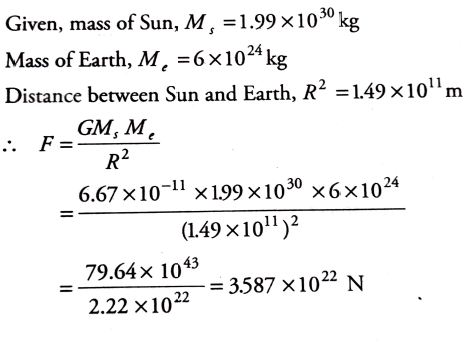
3 ] Find the acceleration due to gravity on the surface of Jupiter using the data given below;

(Mass of Jupiter: M = 1.9 x 10^27 kg,
the radius of Jupiter = R = 7 x 10^7 m

Solution:

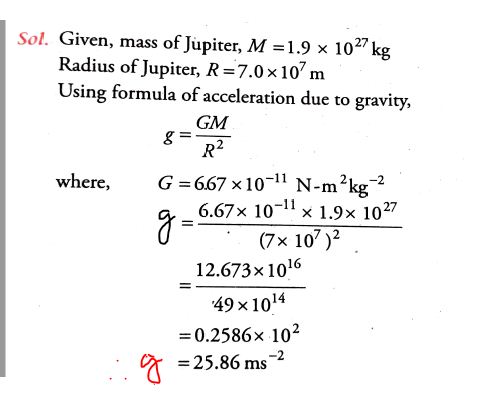
4 ] A body weighs 25 kg on the surface of the earth. if the mass of the earth is 6 x 10^24 kg, the radius of the earth is 6.4 x 10^6 m, and the gravitational constant =6.67 x 10^(-11) N-m^2/kg^2.

Calculate (a) the acceleration produced in the body
(b) the acceleration produced in the earth.

Solution:

5 ] Estimate the gravitational force between 2 protons separated by a distance of 1 angstrom.

mass of proton = 1.6 x 10^(-27) kg

Solution:

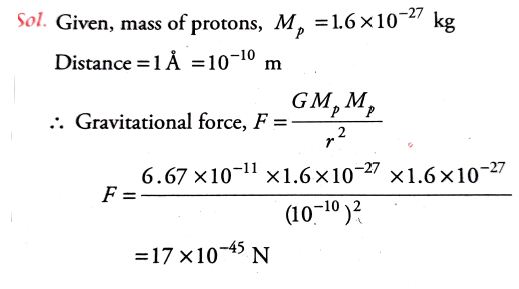
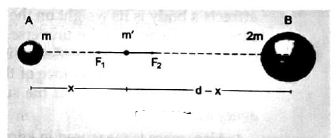
6 ] Two bodies A and B of masses m and 2m respectively are kept at a distance d apart. Where should a small particle be placed, so that the net gravitational force on it due to the bodies A and B is zero?

Solution:

The particle must be placed between A and B bodies, on the line AB, to cancel out the gravitational forces on the particle. Suppose it’s at a distance x from A. So it will be at a distance (d-x) from B. Let its mass is m^I.

7 ] Consider a heavenly body whose mass is half that of the earth and its radius is also half that of the earth. What is the acceleration due to gravity at the surface of this heavenly body? (Take acceleration due to gravity at the surface of the earth = 10 m/s^2)

Solution:

g= GM / R² = [G (M_e/2)]/(R_e/2)² = 2 (G M_e/R_e² ) = 2 g _earth = 2 x 10 m/s² = 20  m/s²

Reference & Related Study

Reference: Newton’s Law of Gravitation

Related Study: Gravitation Class 11 Notes