Solution to problems – class 9 – Set 1 Q 48

Last updated on June 17th, 2019 at 02:46 pm

Problem Statement

48) A ball is thrown vertically upwards from the top of a tower with an initial velocity of 19·6 m/s. The ball reaches the ground after 5 s. Calculate: (i) the height of the tower, (ii) the velocity of ball on reaching the ground. Take g = 9·8 m/s^2

Follow my blog with Bloglovin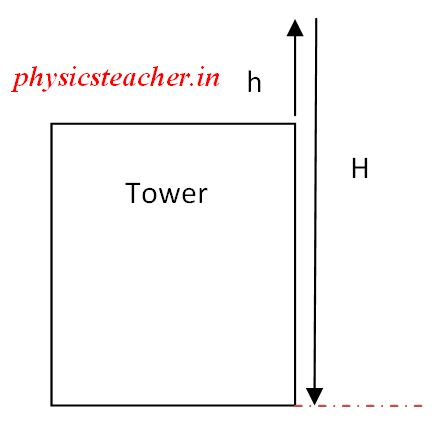

Solution

As the ball is thrown vertically upwards from the top of a tower with an initial velocity of 19·6 m/s, the time taken by the ball to reach the maximum height is = t = u/g = 19.6/9.8 sec = 2 seconds.

And the height it reached with respect to the roof = h = u²/(2g) = 19.6² / (2 x 9.8) = 19.6 m………(1)

Now as per question the ball takes 5 secs to reach the ground after it was thrown upwards.

This means the time taken by the ball to come down from its max height position to the ground = 5 – 2 = 3 seconds.

Therefore, during downward movement the ball traversed a distance say
H= ½ g t² = ½ x 9.8 x 3² = 44.1 m

Now to get the height of the tower we have to deduct the height it rose with respect to the roof from this 44.1 m.

So the height of the tower = H – h = 44.1 – 19.6 = 24.5 m   ………….(answer of i)

The velocity of the ball on reaching the ground V = gt = 9.8 x 3 = 29.4 m/s………(answer of ii)

Question Set – Physics Problems for grade 9