Physics problems with pseudo force and solutions
Last updated on February 12th, 2022 at 02:42 pm
Physics problems with pseudo force with solutions- these problems are going to be related to the noninertial frame of reference.
Let’s solve an interesting numerical.
A smooth inclined plane with an angle of inclination 30 o is moving with a constant acceleration a (as shown in the figure). When a block is placed on the inclined plane, it doesn’t slide down or up the plane. The acceleration a must be:______________
Solution with pseudo force concept:
Here the block is placed on the inclined plane. So the inclined plane will act as the frame of reference for any motion of the block on it.
As the inclined plane is in constant acceleration, we can say that the block is resting on a non-inertial frame of reference.
To solve this kind of numeric problem, we take the help of a concept known as pseudo force.
Let’s draw the force components working on the block using FBD
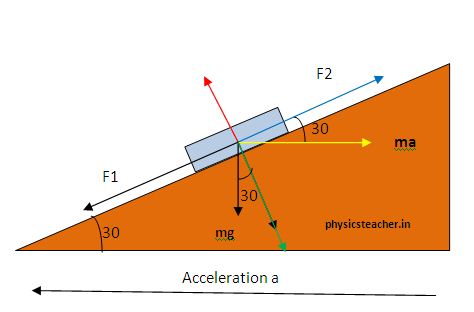
Here, F1 = mg Sin 30 ………….. (1)
where m is the mass of the block resting on the wedge.
F1 is the resolved component of weight mg and F1 tends to drag the block downwards.
As the wedge is at acceleration, it’s to be taken as a non-inertial frame of reference. To solve this kind of problem, the concept of pseudo force helps a lot.
As the wedge moves with a constant acceleration a (from right to left direction as per the diagram), the block on it will appear to have a pseudo force towards the right (when observed by an observer resting on the accelerating wedge itself).
Solution with pseudo force continued…
This pseudo force = mass of the block X acceleration of the observer = ma……….(2)
Now resolved component of this pseudo force along the wedge’s inclined surface =F2.
F2 = ma cos 30 …………….(3)
Now, it’s evident that if F1= F2 then the block won’t slide down or up.
So to have this (from equations 1 and 3),
F1= F2
=> mg Sin 30 = ma cos 30
=> a = g tan 30 = g / 31/2
A good read for u: Elevator and Pseudo force
Get a list of Numerical Problem Sets: Here
