Contact Forces between blocks – Application of Newton’s laws

Last updated on November 18th, 2021 at 02:15 pm

Application of newton’s laws: Newton’s laws of motion give us concepts of force (first law), measurement of force with its equation (second law), and the reaction of force (3rd law).

Today we will discuss an interesting topic of mechanics – the application of Newton’s laws.

It will cover a few interesting applications of Newton’s Laws and analyze different force distribution on blocks in contact ( contact force between two blocks or connected bodies).

We will discuss different situations like when blocks are standing side by side or when one block is resting on another block.

Sometimes there is friction between common surfaces, sometimes not. Sometimes the frame of reference is not inertial. Let’s start with our case 1.

Case 1: Application of Newton’s laws for 2 blocks in contact

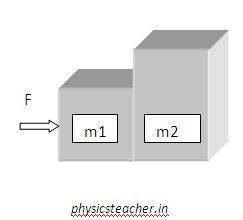
Say, 2 blocks are standing side by side and a force F is applied on one surface of the left block.

The masses of the blocks are shown in the diagram.

Now, what will happen?

How can I get the acceleration of the blocks m1 and m2? What is the net force acting on the block with mass m2?

Solution:

Let’s consider the blocks as a single system and evidently, the mass of that combined system is (m1 +m2).

Now if the acceleration of this system is, say, a then using Newton’s 2^nd law of motion we get:
F = (m1 + m2) a

=>   a = F / (m1 + m2)

This means both the blocks will move with this acceleration.

From this, we can find the fraction of F being applied on the block with mass m2 (at the common surface between the blocks).

This contact force on the block m2 is, say F1.

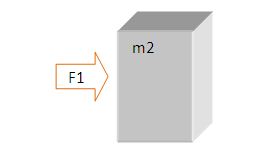
F1= mass of that block x Acceleration of that block = m2 .a = m2. F /(m1 +m2)

As per the diagram, the direction of F1 is left to right (same direction as F)

It clearly shows that block m2 gets a fraction of the force F.

Now following the 3^rd Law of motion, block with mass m2 also exerts an equal and opposite reaction force F2 on the block of mass m1. So F2 = – F1.

So the direction of F2 as per this setup would be from right to left on the block of mass m1.

And the magnitude of F2 would be the same as F1 i.e. m2. F /(m1 +m2)

Now if we consider the free body diagram of the block with mass m1 then see what we find:

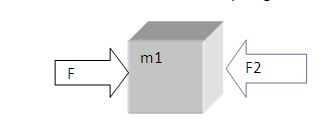
So, net force on the block with mass m1 = F – F2 = F – m2. F /(m1 +m2) = m1. F/(m1 +m2).

We can validate the acceleration from this expression as well.

acceleration of block m1 = net force/mass
=[ m1. F/(m1 +m2)]/m1 = F/(m1 +m2).
It is the same as the one we derived at the beginning.

Case 1 Summary:

The net force on the left block with mass m1
= m1. F/(m1 +m2)

And

The net force on the right block with mass m2
= m2. F/(m1 +m2)

If you add these two net force components you will get the total force F that we started with.

So certainly a horizontal force will get proportionately distributed among the blocks resting side by side according to their masses. To be noted: In this case, we didn’t consider any friction.

Case 2: Application of Newton’s laws for 2 blocks in contact

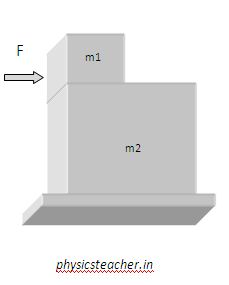
Say a block of mass m1 is resting on another block of mass m2.
Let’s refer to these blocks as block m1 and block m2 respectively for the rest of our discussion.
Block m2 is resting on a surface.

The assumption for this case: There is no friction between the surfaces.

Action: A force F is applied on the block m1 horizontally as shown in the diagram.

Result:

Now, will any component of this force F be transmitted to the block m2, in this case?

Or any side effect of this force F?

Note that, there is no friction between the surfaces of m1 and m2.

Ok, so you have your answers! Let’s check.

1)The force F is horizontal and it doesn’t have any nonzero component towards the block m2.
(component of F towards m2= F cos90 = 0)

2)Without the presence of friction between m1 and m2 and between m2 and the bottommost surface, we don’t have any frictional force as well on m1 and m2.

So only m1 gets a force applied to it in this case.
Acceleration of m1 is: a = F/m1.

Now, m1 will move on m2 towards the right with this acceleration.

m2 doesn’t change in a static condition as it doesn’t face any external force. It’s as per Newton’s first law and this is an example of Inertia of Rest.

Now, if the length of the m2 block is L then the block m1 will traverse the distance L in, say, time t

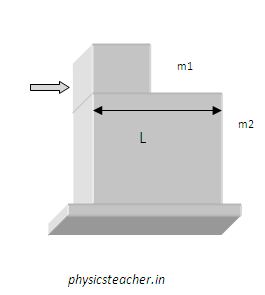
L = (1/2) a t²
t = (2L/a)^1/2    

So after a time duration t = (2L/a)^1/2, m1 block will fall from the roof of m2.

Case 3: Application of Newton’s laws for 2 blocks in contact

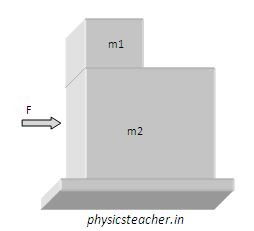
Now, if the force F is applied on the block m2 (the lower block) and if we consider that there is no friction between the surfaces then what will happen?

Similar to the previous case the F won’t have any nonzero component pointing towards m1 as Fcos90 equals zero. There is no friction between the surfaces of m1 and m2; so there won’t be any force component on m1 arising from the frictional ground.

As a result, m2 is the only candidate facing force F.
And as there is no friction between m2 and the bottommost surface, hence the acceleration of the block m2 will be F/m2.

With this acceleration, the m2 block will start moving and it moves ahead without any horizontal movement of the m1 block (no force on it as discussed). Eventually, m1 will fall vertically downwards as the block m2 moves ahead. It’s as per Newton’s first law and this is an example of Inertia of Rest.
I hope these use cases related to blocks in contact have given a good idea of the application of Newton’s laws of motion. You can analyze different such blocks in contact settings and find out how Newton’s laws of motion can be applied there.