Derivation of the Equations of Motion | deriving ‘suvat equations’

Last updated on October 8th, 2023 at 12:37 pm

Derivation of the Equations of Motion: To calculate quantities involving motion in a straight line at a constant acceleration we need four equations. These equations are often informally referred to as the ‘suvat equations’ after the symbols used for the 5 quantities involved.

We will derive equations for the following 5 motion quantities: displacement (s), initial velocity (u), final velocity (v), acceleration (a), and time (t). Before going for the derivation, we will draw a velocity-time graph in the next section.

Derivation of the Equations of Motion (Suvat equations)

Now, let us start with the derivation of SUVAT equations or motion equations. First, we will draw a velocity-time graph, and then using that we will derive the equations of motion (listed in the image below) one by one.

SUVAT EQUATIONS

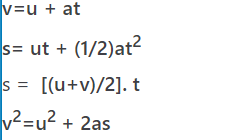
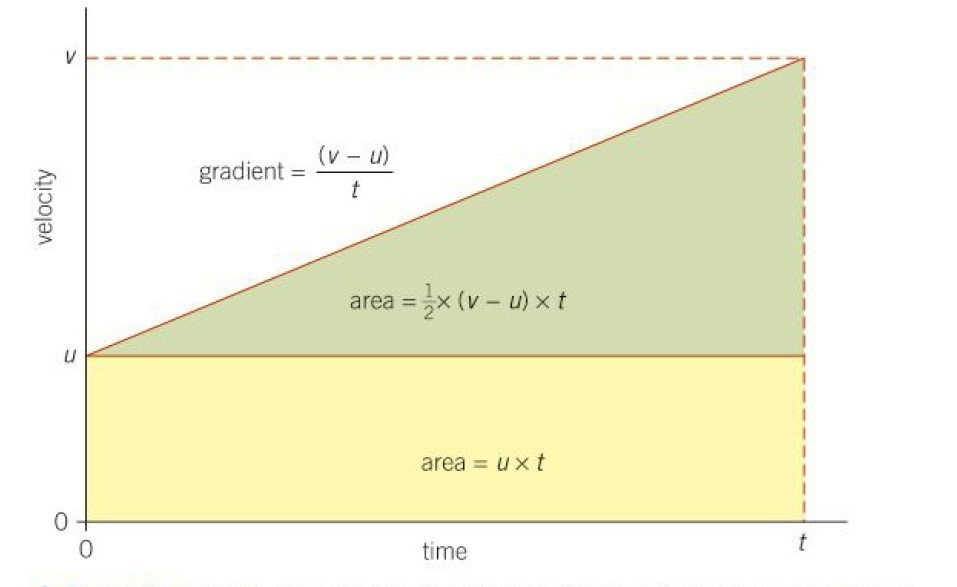
Velocity Time Graph required to derive the motion equations

This velocity time graph depicts the motion of a body in a straight line at a constant acceleration a. It has an initial velocity of u and a final velocity of v.
t is the time elapsed.
During this time duration, the displacement of the body in motion is s.

Derivation of Final Velocity equation (without mentioning displacement)

From the graph above, acceleration a = gradient of velocity-time graph= Δv/Δt = (v-u)/t
=> v=u + at ……………….. (1)
This is the equation of the final velocity v.

Please note that this equation of final velocity doesn’t mention displacement s.

Derivation of Displacement Equation (without mentioning final velocity)

The area under the velocity-time graph is equal to the displacement s.
This v-t area in the above diagram has 2 distinct areas: one rectangular and the other one triangular.

The rectangular area of the velocity time graph = ut
And the triangular area=(1/2).(v-u).t =(1/2).(u+at-u).t=(1/2)at²
So total area under the v-t graph = displacement = s= ut + (1/2)at²
s= ut + (1/2)at² ……….(2)
This is the equation of the displacement s.

Please note that this equation of displacement doesn’t have any mention of final velocity v.

Derivation of Displacement Equation (without mentioning acceleration)

If the area under the graph is taken as the area of a trapezium, then it has u and v as 2 parallel sides of the trapezium, and t is the perpendicular separation between these 2 sides.
So area of this trapezium=s = (1/2)(u+v)t

So displacement = average velocity * time = [(u+v)/2]. t ………..(3)

Please note that this equation of displacement doesn’t have any mention of acceleration a.

Derivation of final velocity Equation (without mention of time)

from equation 1 we get t=(v-u)/a

so in equation (3) replacing t, we get:
s=[(u+v)/2].t = [(v+u)/2].[(v-u)/a] = (v²-u²)/(2.a)
v²-u²=2as => v²=u² + 2as………………(4)
This is another equation of the final velocity v.

Please note that this equation of final velocity doesn’t have any mention of time t.

Summary | Takeaway | Suggested reading

We have derived 4 motion equations involving 5 quantities in easy steps. As we are done with the derivation of the suvat equations, now it’s time to solve some numerical problems of the motion chapter.

Here are suggested posts for your further study and problem-solving.

Motion numerical

Kinematics equations

Numerical sets