Numericals on Conservation of Momentum class 11
Last updated on April 25th, 2023 at 04:01 pm
In this post, we will solve a few selected Numericals on the conservation of momentum class 11. These are basically collision problems in two dimensions. We will solve this momentum conservation numerical set by representing the collision problems with axial-vector components and using the law of conservation of momentum.
Conservation of momentum in all closed systems is valid, regardless of the directions of the objects before and after they collide. Most objects are not confined to a single line, like trains on a rail. Rather, many objects, like billiard balls or cars, can move in two dimensions. The conservation of momentum for these objects can also be calculated.
Momentum is a vector and collisions of objects in two dimensions can be represented by axial-vector components. To review axial components, revisit posts on Resolving Vectors into Axial Components and Vector Addition. Here we start solving the collision numerical set.
Numericals on Conservation of Momentum class 11 – solved
Example Problem #1: A 2.0 kg ball, A, is moving with a velocity of 5.00 m/s due west. It collides with a stationary ball, B, also with a mass of 2.0 kg. After the collision, ball A moves off at 30° south of west while ball B moves off at 60° north of west. Find the velocities of both balls after the collision.
Solution: Since ball B is stationary before the collision, then the total momentum before the collision is equal to the momentum of ball A.
The momentum of ball A before the collision is shown in red below, and can be calculated to be:
p = mv = (2.00 kg)(5.00 m/s) = 10.0 kg m/s west
Example Problem #1: A 2.0 kg ball, A, is moving with a velocity of 5.00 m/s due west. It collides with a stationary ball, B, also with a mass of 2.0 kg. After the collision, ball A moves off at 30° south of west while ball B moves off at 60° north of west. Find the velocities of both balls after the collision.
Solution: Since ball B is stationary before the collision, then the total momentum before the collision is equal to the momentum of ball A.
The momentum of ball A before the collision is shown in red below, and can be calculated to be:
p = mv = (2.00 kg)(5.00 m/s) = 10.0 kg m/s west
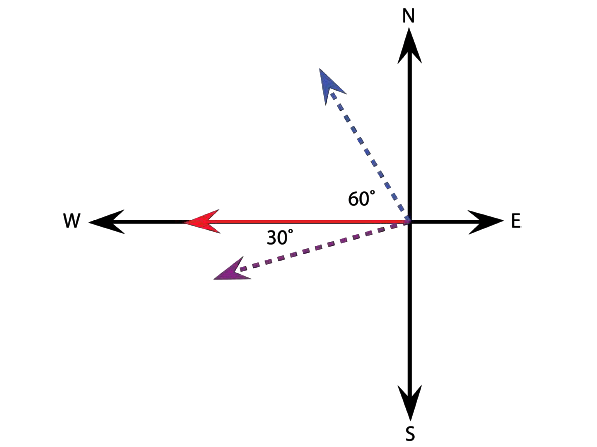
Since momentum is conserved in this collision, total momenta after the collision = total momenta before the collision = 10.0 kg m/s west.
In other words, the vector sum of the momenta of balls A and B after the collision must be 10.0 kg m/s west.
Now as after collision both A and B have their individual momentum, we can get those by resolving their vector sum value (10.0 kg m/s west), according to their directions after the collision, as directed by the problem statement (also see figure 1 above).
Momentum of A after the collision = PAfinal = (10.0 kg m/s)(cos30) = (10.0 kg m/s)(0.866) = 8.66 kg m/s
And, Momentum of B after the collision =PBfinal = (10.0 kg m/s)(cos60) = (10.0 kg m/s)(0.500) = 5.00 kg m/s
To find the final velocities of the two balls, we divide the momentum of each by its mass.
Therefore, final velocity of A = VA = PAfinal / mass of A = (8.66/2) m/s = 4.3 m/s
and final velocity of B = VB = PBfinal / mass of B = (5/2) m/s = 2.5 m/s .
Example Problem #2: A 1325 kg car moving north at 27.0 m/s collides with a 2165 kg car moving east at 17.0 m/s. The two cars stick together after the collision. What is the speed and direction of the two cars after the collision?
Solution:
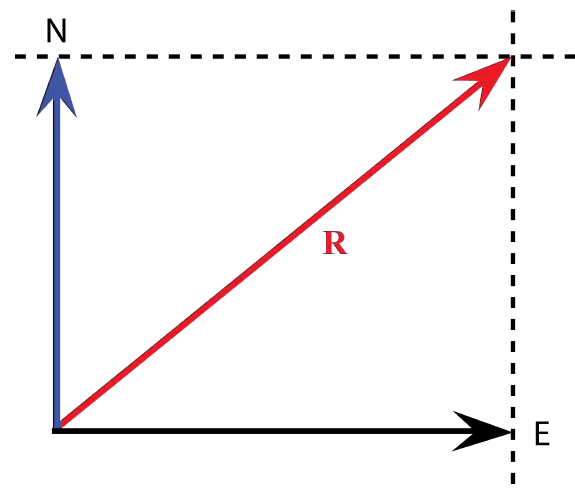
Before collision Northward momentum = (1325 kg)(27.0 m/s) = 35800 kg m/s
Before collision Eastward momentum = (2165 kg)(17.0 m/s) = 36800 kg m/s
Hence, Magnitude of Net momentum before collision = R =√[(35800)2+(36800)2] = 51400 kg.m/s
Direction of Net momentum before collision: θ = tan-1 (35800/36800) = 44° north of east
As per the law of conservation of momentum, the momentum after collision = momentum before collision.
Hence, after collision momentum of the two cars (that got stuck after collision) = 51400 kg.m/s in the direction 44° north of east Therefore, the velocity of two cars in combined condition after the collision = momentum/mass = 51400/(1325+2165) m/s = 51400/3490 m/s = 14.7 m/s @ 44° N of E
Example Problem #3:
A 6.00 kg ball, A, moving at a velocity of 3.00 m/s due east collides with a 6.00 kg ball, B, at rest. After the collision, A moves off at 40.0° N of E and ball B moves off at 50.0° S of E.
a. What is the momentum of A after the collision?
b. What is the momentum of B after the collision?
c. What are the velocities of the two balls after the collision?
Solution:


More Explanation coming soon.
Related study (collisions)
Collisions – definitions, types, sample numerical
Numerical problems – collisions
Numerical problems – 2D collisions
