Newton’s Cradle & Momentum Conservation
Last updated on September 15th, 2021 at 02:31 pm

Using Newton’s Cradle apparatus very familiar example of momentum conservation is demonstrated. The law of Conservation of Momentum states that the change in the total momentum of a system is zero when the net force on the system is zero. With the help of Newton’s Cradle, we can demonstrate the conservation of momentum with a set of hanging balls. The details are provided in the section below.
Conservation of momentum from Newton’s Second Law – the principle behind Newton’s Cradle
We now consider the conservation of momentum by referring back to Newton’s Second Law (N2L). As a reminder, N2L states that a net force on a mass m will accelerate the mass m, that is ΣF = Fnet = ma …………… (i)
When we discussed impulses, we rewrote N2L as F = (mVf – mVi)/Δt
FΔt = mVf – mVi = Δp ……………..(ii)
F represents the net force on the object (or system) in question. The equation states that if the net force on the system is zero, the change in momentum of the system must also be zero.
From equation (ii), when F=0 then mVf= mVi
=> pi = pf
Here, we have been led to the conclusion that the initial momentum of the system equals the final momentum of the system (pi = pf ) if the net force on the system is zero.
In general, for any isolated system, the change in the total momentum of the system is zero. As long as this condition holds, the momentum of a system with any number of interacting objects is conserved.
Reference & suggested study for the readers: Law of conservation of momentum
How does Newton’s Cradle demonstrate the conservation of momentum?
A very familiar example of momentum conservation is demonstrated using a “Newton’s Cradle” apparatus ( see Figure), but the same conservation principle can be easily demonstrated using two identical marbles or two identical coins.

As seen in the above Figure of Newton’s cradle, the ball on the left is permitted to swing into the remaining hanging balls, and the ball on the right swings out. We say the momentum of the left ball has been transferred to the momentum of the right ball. The momentum is actually transferred through each of the balls. Then again the right ball swings back into the series of hanging balls, and its momentum is transferred through each ball in the series, and the ball on the left swings out.
Understanding Newton’s Cradle and conservation of momentum in a simpler way – using 2 identical marbles
The conservation of momentum in Newton’s cradle can be demonstrated with two identical marbles in a simpler manner.
One is at rest and one is in motion, causing a head-on collision with the marble at rest. We solve this problem (and all others, unless stated otherwise) assuming that the interacting objects form an isolated system.
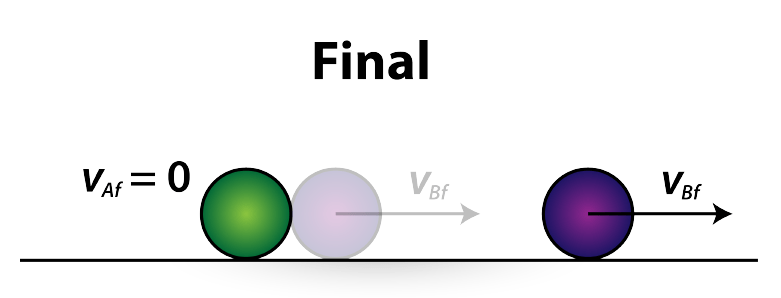
In Figure 2, marble A has mass m and moves with velocity VAi along a horizontal surface toward marble B with mass m, and initial velocity VBi = 0. After the collision ( Figure 2), marble A is at rest and marble B is moving with the final velocity VBf .
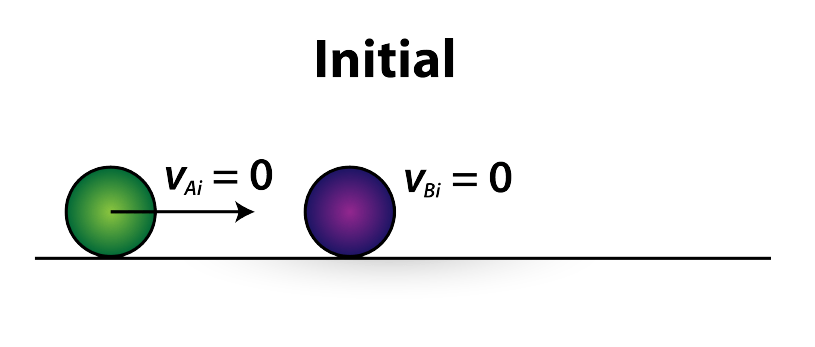
Using Conservation of Momentum, we first write the initial momentum of the system, pi, and then write the final momentum of the system pf. Once these quantities are known, we use the conservation of momentum pi = pf.
pi = mVAi+mVBi = mVAi+m.(0) = mVAi
pf= mVAf +mVBf = m.(0)+mVBf
pi = pf
or, mVAi = mVBf =>VAi = VBf
We find the final velocity of marble B is the same as the initial velocity of marble A.
In other words, all of the momentum of marble A has been transferred to marble B.
You can get a feel for the truth of this result using two identical coins. What you’ll see when you have them collide head-on is that the first coin will stop and the second coin will move.
This same incident happens for Newton’s cradle when each ball hit’s the next ball in the series and transfers its momentum to it.
However, because of the effect of friction between the coins and the surface, you will not be able to see the target coin move along with the same velocity as the incoming coin.
