Friction Numericals – class 11 physics
Last updated on June 7th, 2023 at 02:46 pm
Here we will solve a set of Friction Numericals based on the concepts of frictional force or friction and friction coefficient for class 11 and class 12 students.
Here are the links to the posts on friction and friction coefficient, that you can visit and read for better understanding.
Important Concepts of Friction [that helps to solve the numericals]
• Friction is caused by bodies sliding over rough surfaces.
• The degree of surface roughness is indicated by the coefficient of friction, μ.
• The force of friction is calculated by multiplying the coefficient of friction by the normal force.
• The frictional force always opposes motion.
• Acceleration is caused by the net force which is found by subtracting the frictional force from the applied force.
Friction Numericals | Numericals based on friction class 11
Let’s solve some numerical problems using the concepts and formula of friction.
[Numerical Problem 1] A box weighing 2000 N is sliding across a cement floor. The force pushing the box is 500 N and the coefficient of sliding friction between the box and the floor is 0.20. What is the acceleration of the box?
Solution:
In this case, the normal force for the box is its weight.
Using the normal force and the coefficient of friction, we can find the frictional force.
We can also find the mass of the box from its weight since we know the acceleration due to gravity.
Then we can find the net force and the acceleration.
Friction = FF = μFN = (0.20)(2000 N) = 400 NMass of box = weight/g = (2000 / 9.8) Kg = 204 Kg
Fnet = Pushing force – frictional force = 500 N – 400 N = 100 N
Acceleration = a = Fnet / mass = (100 / 204 ) m/s2 = 0.49 m/s2
[Numerical Problem 2] Two boxes are connected by a rope running over a pulley (see image). The coefficient of sliding friction between box A and the table is 0.20. (Ignore the masses of the rope and the pulley and any friction in the pulley.) The mass of box A is 5.0 kg and the mass of box B is 2.0 kg. The entire system (both boxes) will move together with the same acceleration and velocity.
Find the acceleration of the system.
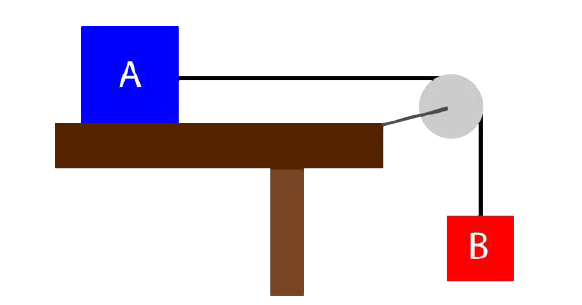
Solution:
The force tending to move the system is the weight of box B and the force resisting the movement is the force of friction between the table and box A.
The mass of the system would be the sum of the masses of both boxes. The acceleration of the system will be found by dividing the net force by the total mass.
FN(box A) = mg = (5.0 kg)(9.8 m/s^2) = 49 N
Friction = FF= μFN = (0.20)(49 N) = 9.8 N
Weight of box B = mg = (2.0 kg)(9.8 m/s^2) = 19.6 N
Fnet = 19.6 N – 9.8 N = 9.8 N
a = Fnet / (total mass of A and B) = 9.8 N/7.0 kg = 1.4 m/s^2
Suggestion:
If you need quick guidance on ‘pulley-based numerical problems’ like the above one, then you can go through this post on pulley problems – how to address pulley numerical problems
Friction Numerical Extra Questions for class 11 – with Solution Link
[Extra Numerical Problem 1] A 52 N sled is pulled across a cement sidewalk at a constant speed. A horizontal force of 36 N is exerted. What is the coefficient of sliding friction between the sidewalk and the metal runners of the sled?
Extra numerical Problem 1: Solution Link
[Extra Numerical Problem 2] If the coefficient of sliding friction between a 25 kg crate and the floor is 0.45, how much force is required to move the crate at a constant velocity across the floor?
Extra numerical Problem 2: Answer & Solution Link
[Extra Numerical Problem 3] A smooth wooden 40.0 N block is placed on a smooth wooden table. A force of 14.0 N is required to keep the block moving at constant velocity.
(a) What is the coefficient of sliding friction between the block and the tabletop?
(b) If a 20.0 N brick is placed on top of the wooden block, what force will be required to keep the block and brick moving at constant velocity?Friction extra numerical problem 3: Answer and Solution Link
[Extra Numerical Problem 4] A 4000 kg truck is parked on a 15 degrees slope. How big is the friction force on the truck?
[Extra Numerical Problem 5] A block of mass 0.500 kg slides on a flat smooth surface with a speed of 2.80 m/s. It then slides over a rough surface with μk and slows to a halt. While the block is slowing, (a) what is the frictional force on the block? (b) What is the magnitude of the block’s acceleration? (c) How far does the block slide on the rough part before it comes to a halt?
[Extra Numerical Problem 6] A block slides down a rough incline sloped at an angle of 40.0 degrees from the horizontal. Starting from rest, it slides a distance of 0.800m down the slope in 0.600 s. What is the coefficient of kinetic friction for the block and surface?
Solution: [ take this as your assignment for now. Will add the solution soon]
[Extra Numerical Problem 7] A factory uses a motor and a cable to drag a 300 kg machine to the proper place on the factory floor. What power must the motor supply to drag the machine at a speed of 0.50 m/s? The coefficient of friction between the machine and the floor is 0.60.
[ExtraNumerical Problem 8] A 1500 kg car has a front profile that is 1.6 m wide by 1.4 m high and a drag coefficient of 0.50. The coefficient of rolling friction is 0.02.
What power must the engine provide to drive at a steady 30 m/s if 25% of the power is “lost” before reaching the drive wheels?
