Rocket Equation Derivation along with Rocket Acceleration formula

Last updated on April 15th, 2021 at 02:42 pm

Rocket Equation Derivation is the objective of this post. We will also derive the Rocket Acceleration formula here as we go forward. When the fuel of rocket burns the fuel gas gets expelled backward at a high velocity. This results in a force being applied on the rocket in the forward direction and the rocket accelerates.

Here we will derive the rocket equation and in this process, the formula of the rocket acceleration will also be derived.

Rocket Equation Derivation + Rocket Acceleration formula

If you want to quickly brush up how a rocket works and how the principle of conservation of momentum works then this post will help you: How rockets work

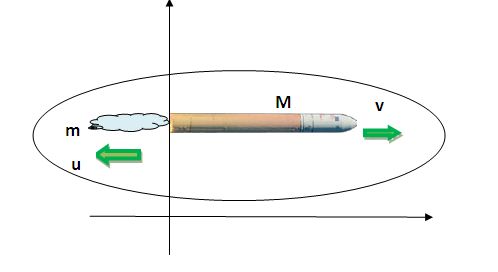
Say, at some instant, the rocket mass is M (i.e., M is the mass of the rocket body plus the mass of the fuel at that point in time).  

Right at that instant, say, the rocket’s velocity is v (in the +x direction); this velocity is measured relative to an inertial reference system (the Earth, for example). Thus, the initial momentum of the system is p_i = Mv………………..(1)

The rocket’s engines are burning fuel and ejecting the exhaust gases in the –x direction. Say, during an infinitesimal time interval dt, the engines eject a gas of infinitesimal mass m at velocity –u.

 Note that although the rocket velocity v is measured with respect to Earth, the exhaust gas velocity is measured with respect to the (moving) rocket. Measured with respect to the Earth, therefore, the exhaust gas has velocity (v − u).

Here all the velocities are along the X-axis (positive and negative of X-axis), and hence vector notation is not used for simplicity.

As a consequence of the ejection of the fuel gas, the rocket’s mass decreases by m, and its velocity increases by dv.
Therefore, including both the change for the rocket and the change for the exhaust gas, the final momentum of the system is p_final = p_rocket + p_gas
= (M-m)(v + dv) + m(v-u)

Applying conservation of momentum, we obtain
p_i = p_f

Mv = (M-m)(v + dv) + m(v-u)
Mv = Mv + M dv – mv – m dv + mv –mu
Mv = Mv + M dv – m dv – mu
0 = M dv – m dv – mu

Here m dv is very small and negligible, So
0 = M dv– mu
M dv = m u …………………(2)
since m represents an increase in the mass of ejected gases, it must also represent a decrease of mass of the rocket:

m = − dM.
So, from eqn 2 we can write, M dv = − dM u
dv = − (u/M)(dM)……(3)

To get the acceleration, a = dv/dt = − (u/M)(dM/dt)…..(4)

So we get the formula of rocket acceleration here, as
a = − (u/M)(dM/dt)

Now From ( Eqn 3):
Integrating from the initial mass M_i to the final mass M_f of the rocket gives us the result we are after.
[ here, v_i is the initial velocity and v_f is the final velocity of the rocket.
And u is the velocity of the exhaust fuel gases (as shown in the diagram above)]

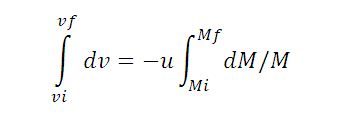
v_f – v_i = u ln (M_i/M_f)
Change in Velocity = Δv= u ln (M_i/M_f) …………(5)

This equation is called the rocket equation.

It was originally derived by the Soviet physicist Konstantin Tsiolkovsky in 1897.

It gives us the change of velocity that the rocket obtains from burning a mass of fuel that decreases the total rocket mass from M_i down to M_f.

It shows that the relationship between Δv and the change of mass of the rocket is nonlinear.

Rocket Equation

Change in Velocity of the rocket= Δv= u ln (M_i/M_f)

[change of velocity that the rocket obtains from burning a mass of fuel that decreases the total rocket mass from M_i down to M_f]

The formula of rocket acceleration

a = − (u/M)(dM/dt)