Explosion and Conservation of Momentum
An explosion can be thought of as a single object separating into two or more fragments. In this post, we will see if the law of conservation of momentum is maintained during an explosion. We will solve related numerical problems as well.
Some familiar examples of explosions are:
- a bomb blowing into fragments
- a bullet shot out of a gun
- water streaming out of a hose
- an alpha particle ejected out of a nucleus
- blood pumping out of your heart.
Law of Conservation of Momentum & Explosion
The motion of an exploding object can be determined using conservation of momentum principles. This is because momentum is conserved for all interactions, regardless of whether they are explosions or collisions. On the other hand, kinetic energy is only conserved for elastic interactions – an explosion is definitely not an example of this.
Law of Conservation of momentum is maintained when an explosion happens.
If there is no external unbalanced force acting on an object (all forces were internal), we have a closed system and there would be no change in the total momentum of the system if an explosion happens to that object. In other words, the total momentum before the explosion = total momentum after the explosion. That means, the Law of Conservation of momentum is maintained when an explosion happens.
Solved Numerical Problems on Explosion & Conservation of Momentum
1 ) Consider a 10 kg bomb at rest that explodes into two fragments (Figure 1). If a 4 kg piece (m1) travels west at 15 m s–1 (v1), then show that the 6 kg piece (m2) would have moved in the opposite direction (at a speed v2).
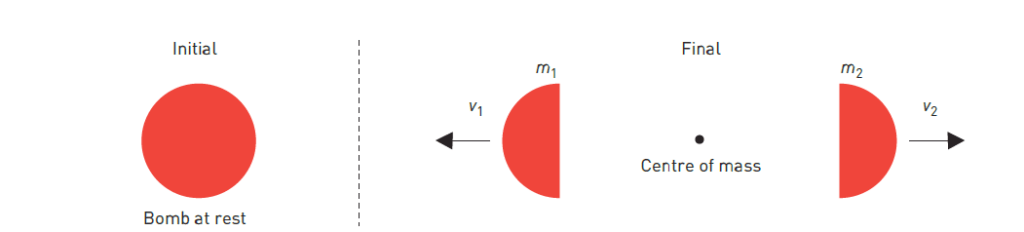
Solution:
As there were no external unbalanced forces acting on the bomb (all forces were internal), we have a closed system and there would be no change in the total momentum of the system. This is the law of conservation of momentum.
p before = p after
(m v)before = (m v)after (law of conservation of momentum)
( m 1 + m 2 ) u = m 1 v 1 + m 2 v 2
10 × 0 = 4 × 15 + 6 × v 2
v 2 = − 10 ms −1 (the negative sign means east)
2 ) A boy on roller-skates is traveling along at 8 m s–1. He has a mass of 60 kg and is carrying his schoolbag of mass 10 kg. He throws the bag directly forward at 20 m s–1 relative to the ground. Calculate the boy’s speed after the ‘explosion’.
Solution
The boy and the bag have initial velocities in the positive direction. The final velocity of the bag is also positive.
p before = p after
=>( m 1 + m 2 ) u = m 1 v 1 + m 2 v 2
( 60 + 10 ) × 8 = 60 × v 1 + 10 × 20
=> 560 = 60 × v 1 + 200
=>v 1 = + 6 ms −1
The positive direction means that the boy would continue to move forward.
