Collisions and Newton’s Laws of Motion – How to relate these?
Last updated on November 21st, 2021 at 10:07 am
This post covers how Collisions and Newton’s Laws of Motion are related. As collisions, we can take examples of the interaction between two bodies (gun-bullet, skater-skateboard, hose-water).
For simplicity let us consider a simple collision between two balls and find out how Newton’s Laws of Motion can be applied to analyze the events related to a collision.
Collisions and Newton’s Laws of Motion
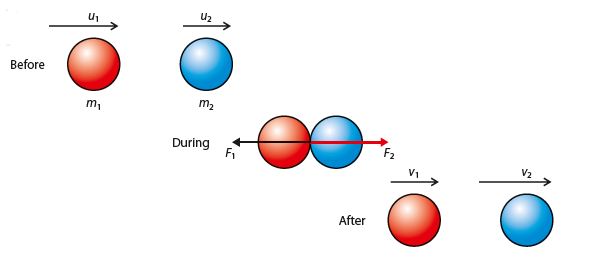
Let us apply Newton’s three laws to this problem.
Newton’s first law is applied during a collision – how?
As per the diagram above, the red ball of mass m1 is moving towards the right with u1 velocity, and the blue ball of mass m2 is also moving towards the right but with a velocity u2 .
In the collision, the red ball slows down to v1 and the blue ball speeds up to v2. Newton’s first law tells us that this means there is a force acting on the red ball (F1) directing towards the left (against its motion) and thus the red ball slows down.
Similarly, a force is acting on the blue ball (F2) directing towards the right (along its initial direction) and helps the blue ball to speed up.
This is what is said in Newton’s first law of motion, that a force is required to change the velocity of a motion.
Newton’s second law is applied during a collision – how?
This law tells us that the force will be equal to the rate of change of momentum of the balls involved. now if the balls are touching each other for a time ∆t.
So we can write, F1 = (m1v1 -m1u1) / ∆t ……… (1)
and, F2 = (m2v2 -m2u2) / ∆t ……… (2)
Newton’s third law is applied during a collision – how?
According to the third law, if the red ball exerts a force on the blue ball, then the blue ball will exert an equal and opposite force on the red ball.
That means, F1 = – F2
From equation (1) and (2) we can write,
(m1v1 -m1u1) / ∆t = – (m2v2 -m2u2) / ∆t
=> m1u1 + m2u2 = m1v1 + m2v2
In other words, the total momentum before the collision = total momentum after the collision.
This is what is stated by the Law of conservation of linear momentum.
Related study (collisions)
Collisions – definitions, types, sample numerical
Numerical problems – collisions
Numerical problems – 2D collisions
