How to solve projectile motion problems using Conservation of energy

Last updated on September 24th, 2021 at 03:33 pm

In some situations, the use of conservation of energy can be a much simpler method to solve projectile motion problems than using the kinematics equations. Solving projectile motion problems makes use of the fact that E_k + E_p = constant at every point in the object’s flight (assuming no loss of energy due to friction).

In other words, at each and every point of the projectile trajectory, the sum of kinetic energy and potential energy remains constant, if we assume there is no loss of energy due to friction. In this post, we will use this concept to solve a sample numerical problem of the projectile motion.

Conservation of energy in projectile motion

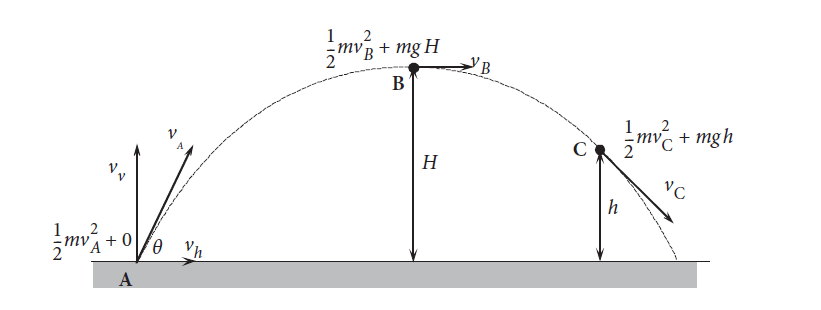
In Figure 1, using the conservation of energy principle we can write the following equation:
Total energy at A = Total energy at B = Total energy at C

(½) m v_A² = (½) m v_B² + mgH = (½) m v_C² + mgh

Solving a projectile numerical using Conservation of energy

A ball is projected at 50 m/s at an angle of 40° above the horizontal. The ball is released 2.00 m above ground level.
Taking g = 10 m/s², determine:
(a) the maximum height reached by the ball
(b) the speed of the ball as it hits the ground

Solution:

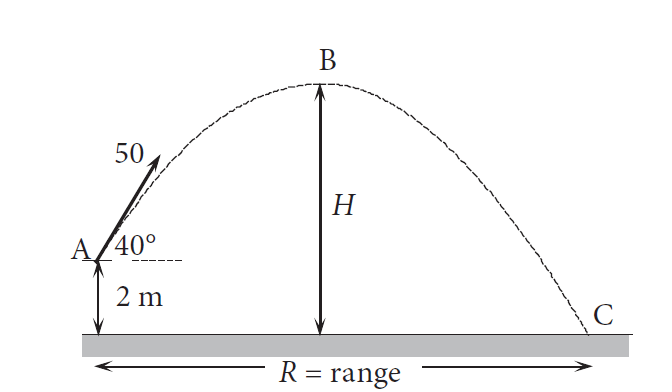
a) The total energy at A = E_k + E_p = (½) m (50)² + mg x 2.00 = 1250 m + m x 10x 2= 1270 m ……… (1)

Next, to find the total energy at B we need to first determine the speed at B, which is given by the horizontal component of the speed at A.
Horizontal component: 50 cos 40° = 38.3 m/s

Therefore, total energy at B = E_k + E_p = (½) m (38.3)² + mg x H = 733.53 m + 10 mH …… (2)

Now, following the conservation of energy principle, we can write from equations (1) and (2):
1270 m = 733.53 m + 10 mH

=> H = 53.6 m

Hence, the maximum height reached by the ball = 53.6 m

b)

At C, the total energy is given by = E_k + E_p = (½) m ( v_C )² + mg x 0 = (½) m ( v_C )² ……….. (3)

Using equations (1) and (3):

1270 m = (½) m ( v_C )²

v_C = 50.4 m/s

So, the ball hits the ground with a speed of 50.4 m/s.