Numerical Problems on Collisions (Elastic & inelastic collision) physics
Last updated on May 30th, 2022 at 12:06 pm
Here is a numerical worksheet based on Collision physics that includes numerical problems related to elastic and inelastic collisions.
Here is another set of solved numerical problems you must try to solve yourself: Collision 2d numerical.
Numerical Problems on collisions (Elastic & inelastic collision)
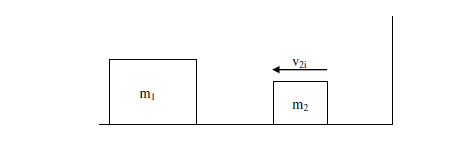
1 ) A block of mass m1 is at rest on a long frictionless table, one end of which is terminated in a wall. Another block of mass m2 is placed between the first block and the wall and set in motion to the left with constant speed v2i. Assuming that all collisions are completely elastic, find the value of m2 for which both blocks move with the same velocity after m2 has collided once with m1 and once with the wall. Assume the wall has infinite mass.
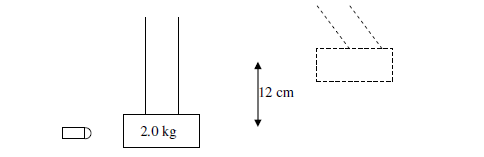
2 ) A bullet of mass 10 g strikes a ballistic pendulum of mass 2.0 kg. The center of mass of the pendulum rises a vertical distance of 12 cm. Assuming that the bullet remains embedded in the pendulum, calculate its initial speed.
3 ) A 5.0 kg particle with a velocity of 3.0 m/s collides with a 10 kg particle that has a velocity of 2.0 m/s in the same direction. After the collision, the 10 kg particle is observed to be traveling in the original direction with a speed of 4.0 m/s. (a) Calculate the velocity of the 5.0 kg particle immediately after the collision. (b) By how much does the total kinetic energy of the system of two particles change because of the collision? (c) How might you account for your answer in b)?
4 ) Two particles, one having twice the mass of the other, are held together with a compressed spring between them. The energy stored in the spring is 60 J. How much kinetic energy does each particle have after they are released? Assume that all stored energy is transferred to the particles and that neither particle is attached to the spring after they are released.
5) A 35 ton railroad freight car collides with a stationary caboose car. They couple together and 27% of the initial kinetic energy is dissipated as heat, sound, vibrations, and so on. Find the weight of the caboose.
[Here is another set of numerical problems for you: Collision 2d numerical]
6 ) An alpha particle collides with an oxygen nucleus, initially at rest. The particle is scattered at an angle of 64 degree above its initial direction of motion and the oxygen nucleus recoils at an angle of 51 degree below this initial direction. The final speed of the nucleus is 1.2 x 10^5 m/s. Calculate the final speed of the particle. (The mass of an alpha particle is 4.0 u and the mass of an oxygen nucleus is 16 u.)
7 ) Two vehicles A and B are traveling west and south, respectively, toward the same intersection where they collide and lock together. Before the collision, A (total weight 2700 lb.) is moving with a speed of 40 mi/h and B (total weight 3600 lb.) has a speed of 60 mi/h. Find the magnitude and direction of the velocity of the (interlocked) vehicles immediately after the collision.
8 ) Two balls A and B, having different but unknown masses, collide. A is initially at rest and B has a speed v. After collision, B has a speed v/2 and moves at right angles to its original motion. (a) Find the direction in which ball A moves after the collision. (b) Can you determine the speed of A from the information given? Explain.
9 ) After a totally inelastic collision, two objects of the same mass and initial speed are found to move away together at half their initial speed. Find the angle between the initial velocities of the objects.
10 ) Two pendulums each of length L are initially situated as shown below. The first pendulum is released and strikes the second. Assume that the collision is completely inelastic and neglect the mass of the strings and any frictional effects. How high does the center of mass rise after the collision?
11 ) A ball of mass m and speed v strikes a wall perpendicularly and rebounds with undiminished speed. (a) If the time of collision is t, calculate the average force exerted by the ball on the wall. (b) Evaluate this average force numerically for a rubber ball with a mass 140 g moving at 7.8 m/s; the duration of the collision is 3.8 ms.
12 ) A 1,400 kg car moving at 5.3 m/s is initially traveling north. After completing a 90 degree right-hand turn in 4.6 s, the inattentive operator drives into a tree, which stops
the car in 350 ms. Calculate the magnitude of the impulse delivered to the car (a) during the turn and (b) during the collision. Calculate the average force acting on the car (c) during the turn and (d) during the collision.
[Here is another set of numerical with solutions for you: Collision 2d numerical]
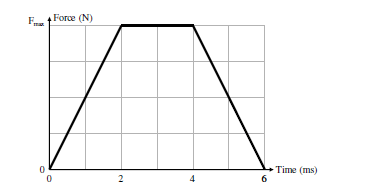
13 ) Below is shown an approximate representation of force vs. time during the collision of a 58 g tennis ball with a wall. The initial velocity of the ball is 34 m/s perpendicular to the wall; it rebounds with the same speed, also perpendicular to the wall. Calculate the value of Fmax, the maximum value of the contact force during the collision.
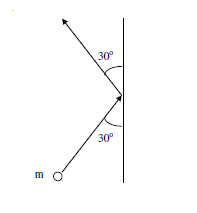
14 ) A 300 g ball with a speed v of 6.0 m/s strikes a wall at an angle of 30 degree and then
rebounds with the same speed and angle. It is in contact with the wall for 10 ms.
(a) Calculate the impulse experienced by the ball. (b) Calculate the average force exerted by the ball on the wall.
15 ) A force exerts an impulse J on an object of mass m, changing its speed from v to u. The force and the object’s motion are along the same straight line. Show that
the work done by the force is (1/2) J (u + v)
16 ) An electron collides elastically with a hydrogen atom initially at rest. The initial and final motions are along the same straight line. What fraction of the electron’s initial kinetic energy is transferred to the hydrogen atom? The mass of the hydrogen atom is 1840 times the mass of the electron.
17 ) A body of 2.0 kg mass makes an elastic collision with another body at rest and continues to move in the original direction but with one-fourth of its original speed. Calculate the mass of the struck body.
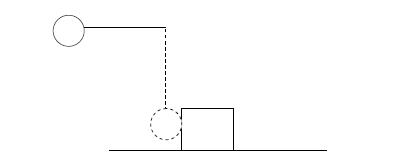
18 ) A steel ball of mass 0.50 kg is fastened to a cord 70 cm long and is released when
the cord is horizontal. At the bottom of its path, the ball strikes a 2.5 kg steel block initially at rest on a frictionless surface. The collision is elastic. Find (a) the speed of the ball and (b) the speed of the block, both just after the collision.
(Sources include good books and standard websites. Our thanks to them.)
Related study (collisions)
Collisions – definitions, types, sample numerical
Numerical problems – collisions
Numerical problems – 2D collisions
Collisions & Newton’s Laws of motion
Types of collision, diagram, differences
