Relative Velocity – definition, examples & Vector concepts
Last updated on April 20th, 2023 at 03:01 am
In this post, we will first define the term Relative Velocity, and then understand its necessity and importance to study the motion of an object. We will go through a case study with examples and then go deeper with the help of the Vector concepts.
Relative Velocity
definition of Relative Velocity
Relative velocity: The velocity of an object measured by a moving observer is referred to as the relative velocity. The relative velocity is the difference between the velocity of the object relative to the ground and the velocity of the observer relative to the ground.
Relative Velocity – the importance
Relative Velocity helps us to understand the motion of an object with respect to a frame of reference, be it static or dynamic.
While discussing the motion of objects near the earth’s surface, we take the earth’s surface as the ‘static’ frame of reference. When an object changes its position with respect to this static frame of reference then we say that it is in motion with respect to a viewer on this static frame of reference.
That’s quite evident and easier to understand.
But the situation gets a bit complex if we have to consider the motion of an object with respect to a ‘moving frame of reference’.
For example, to a passenger on a running train, all nearby houses, trees, and other static objects seem to be in motion. That means with respect to that passenger in a running train those objects have a relative velocity, though they are actually motionless or static. The passenger gets the feeling of being static and all other “actually static” objects like trees and houses seem to move backward.
Relative velocity – a case study | Relative Velocity Example
Imagine that you are in a car traveling at a constant velocity of 90 km/h due west on a straight road. The car ahead of you is traveling at a constant speed of 100 km/h in the same direction. Although the velocity of the other car relative to the road is 100 km/h due west, its velocity relative to you is 10 km/h due west.
That is, the velocity of the car relative to you is equal to 100 km/h due west (velocity of the car relative to the ground) minus 90 km/h due west (your velocity relative to the ground): 10 km/h due west. This is illustrated in Figure 1a.
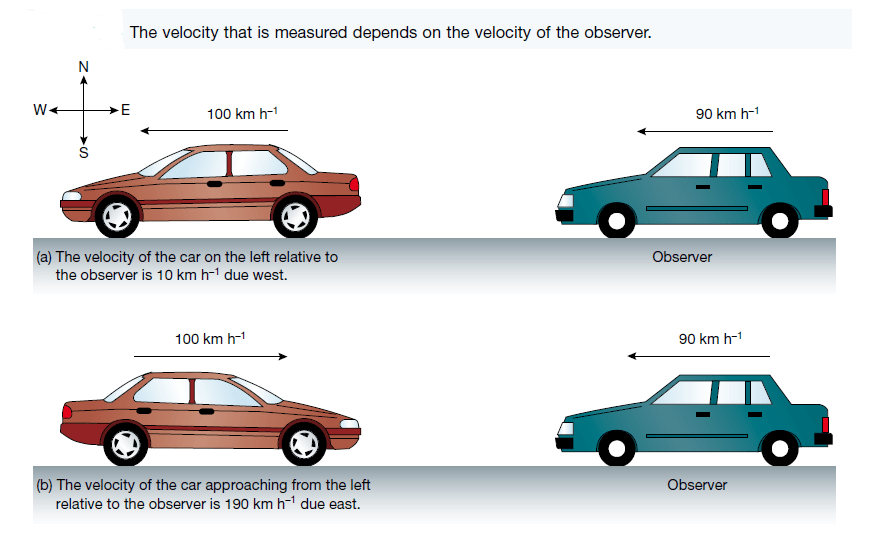
If another vehicle were approaching you at a speed of 100 km/h relative to the road, that is, with a velocity of 100 km/h due east relative to the road, its velocity relative to you would be the difference between 100 km/h due east and 90 km/h due west.
A velocity of 90 km/h due west is the same as −90 km/h due east. The relative velocity is therefore 100 km h−1 due east (velocity of the car relative to the ground) minus −90 km/h due east (your velocity relative to the ground): 190 km/h due east.
This is illustrated in Figure 1b.
Relative Velocity and its Vector concepts
Relative velocity calculation – When we have to calculate the relative velocity of an object with respect to a viewer in motion, we have to subtract the actual velocity of the viewer from the actual velocity of the object. This is kind of making the viewer static forcefully (virtually for calculation) and then measuring the other ‘viewed’ object in this situation.
Say the actual velocity of the object is V1 and the actual velocity of the viewer is V2.
Then the relative velocity of the object with respect to the viewer in motion =Vr = V1 – V2
Now while calculating the difference between V1 and V2, we will use the vector addition process but with a tweak.
It’s here: V1-V2 = V1 + (-V2)
So we have to consider the negative of the V2 vector, which means a vector with the same magnitude as V2 but with a reverse direction.
And then follow the known vector addition process between V1 and (-V2) and get the vector V1-V2. This is what the relative velocity is that we get using the vector subtraction here.
Also Read: (suggested reading)
Difference between Instantaneous Speed and Instantaneous Velocity
Difference between average speed and average velocity
Instantaneous Velocity – definition & equation with solved problem
Average velocity – definition, formula
Instantaneous Acceleration – definition & formula with solved problem
Average Acceleration and its formula & solved numerical problems
