Pulley in Physics – pulley tension problems with solution

Last updated on April 16th, 2021 at 10:06 am

Here in this tutorial, we will study a few pulley systems to find out how to solve pulley tension problems as well. Pulley in Physics is one of the most interesting topics in mechanics. Once you understand the application of Newton’s laws in pulley systems, it may become one of the most favorite topics for you. Pulleys are found on sailboats, on the end of cranes and even in the weight room of a workout gym. Ideal pulleys are considered to be mass-less and frictionless.

How to solve Pulley Tension Problems – setup 1

Question: In the common setup shown in Figure 1, the hanging cylinder of mass m is released from rest.

If the friction between the cart of mass M and the horizontal track is negligible, find the acceleration of the cart and the tension in the rope.

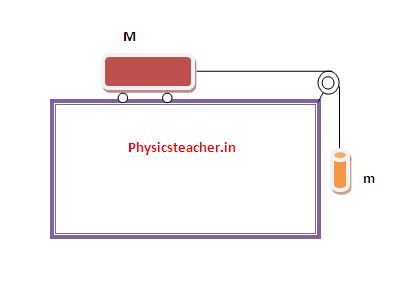
We have to draw one free-body diagram (FBD) for the hanging cylinder and another for the cart.

1. Each subject is represented by a dot (labeled with the mass) in Figures 2 and 3.

– Figure 2 shows the FBD of the cart.
– Figure 3 represents the FBD of the cylinder.

2. Forces are drawn and labeled on each object. No springs or friction is considered.

Coordinate systems and Common acceleration – Pulley in Physics

For an ideal pulley, the tension is the same throughout the rope (therefore the same symbol T in both diagrams).

This is generally a common consideration for pulley tension problems.

The acceleration a of each subject is indicated. The cart accelerates to the right when the cylinder accelerates downward.

Coordinate systems with X-axis and Y axis were used to make calculations easy.

The tight rope ensures that the acceleration of both the cylinder and the cart has the same magnitude.

This choice of coordinates means that the acceleration of both objects is along a positive x-axis (to the right for the cart; downward for the cylinder).

After drawing the FBDs we have to apply Newton’s second law in component form.
– We must write two equations for the cart because there are forces along both x and y directions.

-There is only one equation for the cylinder.

The acceleration of the cart along x must equal the acceleration of the cylinder, so we have used the same symbol a for both.

The cart has no acceleration in the y-direction.

Pulley in Physics – Three forces on the cart

Cart – free body diagram

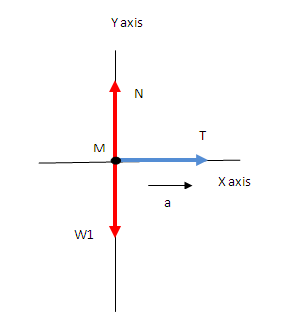
Three forces on the cart (figure 2)

– gravity or weight of the cart W1 = Mg, working vertically downwards

– the normal force N, vertically upwards

– and the tension force T acting through the rope along the positive x-axis, as shown above.

As per this setup of the pulley in physics, there is no movement of the cart along the Y-axis (positive and negative of Y-axis), and the cart only moves along the positive x-axis.

Cart – equations to solve pulley tension problems

Along Y-axis there is no net force, so
N – W1 =0
or, N – Mg =0
or, N = Mg …………………..(1)

Along X-axis, the tension force T gives an accelerated motion to the cart,
T = Ma …………………….(2)

Pulley in physics – Two forces on the cylinder

Cylinder – free body diagram

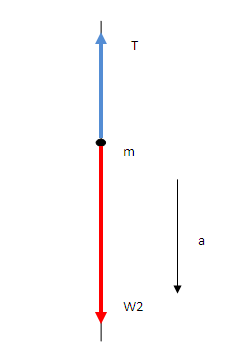
Two forces on the cylinder (figure : 3)

– Gravity or the weight W2 which is equal to mg. [mass of cylinder =m]. This weight mg works vertically downwards.

– The tension force T also works on the cylinder through the string tied with it. Its direction is upwards.

Here the cylinder is with acceleration.

Therefore these two forces are not balanced and there is a net force acting on the cylinder which causes an acceleration of it downwards.

cylinder – equations to solve pulley tension problems

Only one equation and that is along Y-axis.

W2 – T = ma
mg – T = ma ………………..(3)

Now combining equation 2 and 3, we get

mg – Ma = ma
or, a = (mg) /(M+m) ——————–(4)

Here in equation 4, we get the expression of the acceleration of the cylinder and the cart.

Now again from equation 2 and 4 we get a complete expression of the tension T in the rope.

T = Ma = M . (mg) /(M+m)

or, T = (Mmg) /(M+m) …………………….(5)

So the acceleration of the cart is = (mg) /(M+m)

And the tension in the rope is (Mmg) /(M+m)

How to solve Pulley Tension Problems – setup 2

Question: In the common setup shown in Figure 1, the hanging cylinder of mass m is released from rest.

If the friction between the cart of mass M and the horizontal track is present with coefficient of friction μ, find the acceleration of the cart and the tension in the rope.

Pulley in physics – Solution with FBD

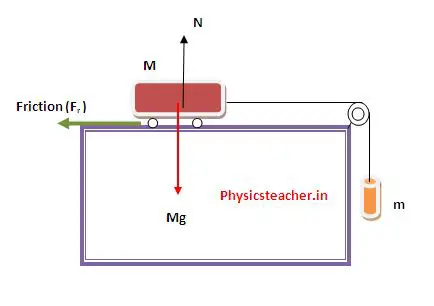
In the previous set up, there was no friction between the cart’s wheels and the table surface below.

But now if we tweak a little bit and consider friction there, then how to solve the problem?

Let the friction coefficient between the above-said surfaces (cartwheel and track) is μ.

Let’s draw the figure again with friction. (figure 4)

See we have shown Mg as the weight of the cart acting vertically downwards.

N is the normal reaction force the track surface applies on the cart vertically upwards.

Here N and Mg balance each other when the cart is on this horizontal table surface.
Therefore, N = Mg


Now, the friction or frictional force that resists movement of the cart is F_r = μ N = μ Mg
Drawing a modified FBD for the cart with mass M:

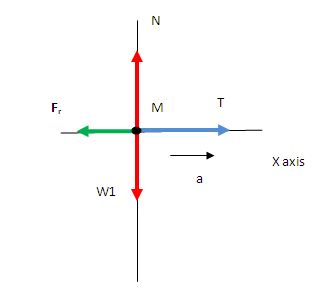
Setting equations for the pulley

For cart M, the equation would be, T – F_r = Ma
or, T – μ Mg = Ma…………… (1)

For the cylinder m the FBD and equation remain same as the previous case.
mg – T = ma …….. (2)

Adding equation 1 and 2,
mg – μ Mg =a(M+m)
or, a = (m – μ M)g/(M+m)

from eqn 2,
 T = m(g-a) = m [g – (m – μ M)g/(M+m)]
= mg [1 – (m – μ M)/(M+m)] = mg[ (M+m-m+ μ M)/(M+m)]
or, T =[Mmg(1 + μ)]/(M+m)

So the acceleration of the cart is
(m – μ M)g/(M+m)

And the tension in the rope is
[Mmg(1 + μ)]/(M+m)

We will add other pulley systems soon and study those as well. If you like this, please share as much as possible.