Apparent weight of moving car over a convex or concave bridge

Last updated on April 16th, 2021 at 10:06 am

Apparent weight of a moving car over a convex or concave bridge is the amount of Normal Reaction the car receives while traveling over the bridge.

Here the system consists of the car, the bridge which is either convex or concave and the motion of the car along the curvature.

So to start off we can write,

Apparent weight of car = N (normal reaction)

In these cases, the centripetal force is to be considered because the car is moving along a circular path while traveling through the concave or convex curvature,

Apparent weight of moving car over a convex bridge

 Let’s consider the motion of the motor car over a convex bridge, along the segment of a circle (i.e. the circular curvature).

Say, the car is just at the midpoint of that circular segment.

As the path of the car at that point is a part of a circle, we can say that the car is having a circular motion along that circular curvature.

And we know that to continue along the circular path, without deviating tangentially, we need a force called centripetal force.

Centripetal force directs towards the center of the circular path.

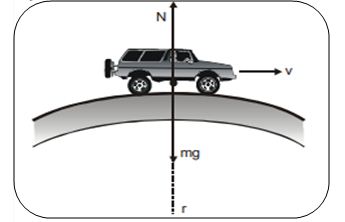
 For the convex bridge, the centripetal force is provided by the difference of weight mg of the car and the normal reaction N of the bridge.

Please note that the center of the circle is below the curvature in this case.

 ∴ for convex bridge

mg – N = mv²/ r
or N = mg – mv²/ r

Clearly N < mg, i.e., the apparent weight of the moving car is less than the weight of the stationary car.

Convex bridge – car is tilted

Now if the car is in a position like the figure below over a convex bridge, then how to find out the N?

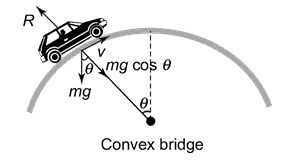
Here,
mg cosθ – N = mv²/ r
or N = mg cosθ – mv²/ r

Apparent weight of moving car over a Concave bridge

Let’s consider the motion of the motor car over a concave bridge, along the segment of a circle (i.e. the circular curvature). Say, the car is just at the midpoint of that circular segment.

Like the above case, here also centripetal force acts on the car to retain it along the circular path. But unlike the above case, this time the center of the circular path is above the bridge.

For the concave bridge, the centripetal force is provided by the difference of the normal reaction N of the bridge and weight mg of the car.

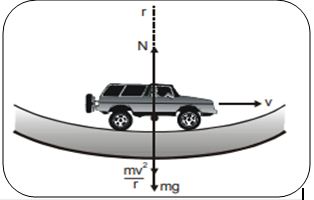
        So for Concave bridge

           N – mg = mv²/ r

   Apparent weight N = mg + mv²/ r

Clearly N > mg, i.e., the apparent weight of the moving car is more than the weight of the stationary car.

Concave bridge – car is tilted

Now if the car is in a position like the figure below over a concave bridge, then how to find out the N?

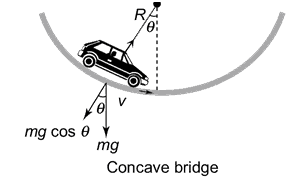
Here, N – mg cosθ = mv²/ r
Apparent weight N = mg cosθ + mv²/ r

Read more related posts