Examples and Practical use of Inelastic collisions
In this post, we will study a few examples of Inelastic collisions. Also, we will study an important practical use of Inelastic collisions.
When objects stick together or are joined together, they are said to be coupled. In a collision where the objects become coupled, the law of conservation of momentum still holds but the mass of the combined body after the collision is equal to the sum of the individual masses of the colliding bodies.
Examples of Inelastic collisions
Some examples of inelastic collisions are:
• an arrow sticking into its target
• two cars colliding head-on.
Practical use of inelastic collisions
One way of measuring bullet speeds is to make use of an inelastic collision.
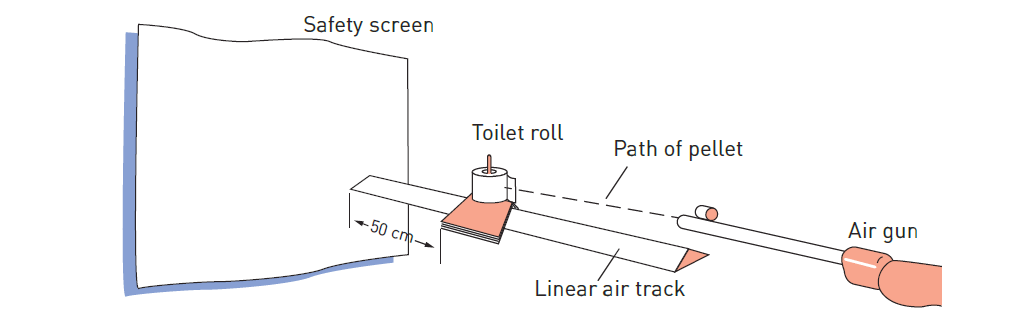
(Measuring the velocity of an air-rifle pellet in the laboratory)
- If an air-rifle pellet is shot into a soft absorbent target (such as a toilet roll) that is attached to a linear air track glider (very low friction), the glider moves away under the impact of the pellet.
- By measuring the time it takes the glider to move a specified distance (50 cm in Figure 1), the velocity of the glider can be determined.
- This data can be used to calculate the velocity of the pellet.
- A device called a ballistic pendulum can be used for measuring the speed of high-speed bullets.
solved Numerical (inelastic collision)
1 ) A supermarket trolley loaded with shopping has a mass of 60 kg. It rolls across the floor at 4 m s–1 and collides with an empty trolley of mass 25 kg, which was stationary. They become fastened together and roll on as one. Calculate the magnitude of the velocity of the two trolleys when locked together.
SOLUTION
Σm v before = Σ m v after
m 1 u 1 + m 2 u 2= m 1 v 1 + m 2 v 2
m 1 u 1 + m 2 u 2 = ( m 1 + m 2 ) v (as v 1 = v 2 )
60 × 4 + 25 × 0= 85 × v
v= 2.8 ms −1
2 ) When a 0.45 g air-rifle pellet is fired into a target attached to a glider on a frictionless linear air track, the glider moves 50 cm in 3.8 seconds. Calculate the magnitude of the velocity of the pellet. The glider and target have a combined mass of 643 g.
SOLUTION
Mass of pellet=0.45 g=4.5× 10–4 kg
Combined mass=643 g=0.643 kg
Velocity of glider= s/t =0.5/38 =0.13 m s–1.
Following the law of conservation of momentum:
Σm v before = Σ m v after
m pellet × u pellet = m target × vtarget
u pellet=m target × v target / m pellet
= 0 .643 × 0.13 /(4.5 × 10−4)
= 186 ms −1
Note: the final mass of the glider and target should include the mass of the embedded pellet but, as it is negligible, it can be ignored in this case. If the mass of the embedded object was large, it would have to be included.

