NCERT Solution of Laws of Motion problems – class 11 physics

Last updated on April 16th, 2021 at 10:07 am

NCERT solutions for class 11 physics chapter 5 laws of motion – This chapter covers selected problems from the chapter laws of motion. Here we are solving selected problems both from the Exemplar and NCERT Physics textbook.

If any problem needs some coverage of fundamentals we are catering that also. We are giving the reference to the question number as well.

Here our approach will be a bit different. We will try to improve the base or the grasp of the topic understanding of our readers by adding some discussions in between. We will add up questions and solutions on a regular basis.

NCERT solutions class 11 – Laws of motion (Exemplary)

1)A girl riding a bicycle along a straight road with a speed of 5 m/s throws a stone of mass 0.5 kg which has a speed of 15 m/s with respect to the ground along her direction of motion. The mass of the girl and bicycle is 50 kg. Does the speed of the bicycle change after the stone is thrown? What is the change in speed, if so?

[NCERT Exemplary Q. 5.16, Page 33]

Ans. Mass of girl and bicycle = m1=50 kg
Mass of stone = m2=0.5 kg

u1 = speed of cycle + girl + a stone, before throwing stone = 5 m/s
v1 = speed of cycle + girl after throwing = ?
v2 = speed of stone = 15 m/s

According to law of conservation of momentum
Initial momentum = Final momentum
Therefore,
(m1 + m2) u1 = m1v1 + m2v2
(50 + 0.5) × 5 = 50 × v1 + 0.5 × 15
50 v1 = 252.5 – 7.5= 245.0
v1 =245/50 = 4.9 m/s
Hence, the speed of cycle decreased by 5 – 4.9 = 0.1 m/s

2)A person of mass 50 kg stands on a weighing scale on a lift. If the lift is descending with a downward acceleration of 9 m s^-2, what would be the reading of the weighing scale? (g = 10 m s^-2)

[NCERT Exemp. Q. 5.17, Page 33]

Say, Apparent weight = Reaction force = R
When lift is descending with an acceleration = a, then,
mg – R = ma
or, R = m (g-a)
So, Apparent weight R = 50(10 – 9) = 50 N
∴ Reading of weighing scale in kgf  = R/g = 50/10 kg= 5 kg

NCERT solutions class 11

3) The position-time graph of a body of mass 2 kg is as given in Fig. What is the impulse on the body at t = 0 s and t = 4 s.

[NCERT Exemp. Q. 5.18, Page 33]

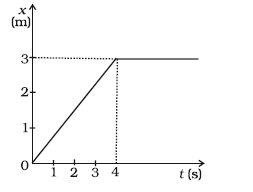
Mass m = 2 kg
From the graph, we can get the slope of the x-t line between t =0 and t=4 s
slope = tan θ= ¾ =0.75

The slope of the x-t graph gives the velocity.
Say, V2= Velocity between t =0 and t=4 s, which is 0.75 m/s.

And say v1= Velocity before t=0 which is 0
And v3 = velocity after t=4 s which is also 0.

Now, Impulse = Ft = m ∆v

So Impulse at t=0 s is m(v2-v1)=2(0.75-0) = 1.5 kg m/s
Impulse at t=4 s is m(v3-v2) = 2(0-0.75) = -1.5 kg m/s

4) The velocity of a body of mass 2 kg as a function of t is given by v(t ) = 2t i +  t² j . Find the momentum and the force acting on it, at time t= 2s.

[NCERT Exemp. Q. 5.20, Page 34]

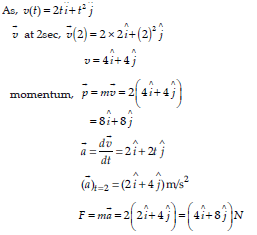
cbse class 11 physics chapter 5 ncert solutions

5) A woman throws an object of mass 500 g with a speed of 25 m s1.
(a) What is the impulse imparted to the object?
(b) If the object hits a wall and rebounds with half the original speed,
what is the change in momentum of the object?

[NCERT Exemp. Q. 5.24, Page 34]

Solution
(a) mass of object, m = 500 g = 0.5 kg
u = 0, v = 25 m/s
Impulse I= Ft = m(v-u)

I = 0.5(25-0) = 12.5 Kg m/s

(b) m = 0.5 kg, u = +25 m/s
v = – 25/2 m/s = -12.5 m/s

So, I = m(v-u)= 0.5(-12.5 – 25)= 0.5(-37.5) = -18.75 kg m/s

6) Two masses of 5 kg and 3 kg are suspended with help of massless inextensible strings as shown in Fig. below. Calculate T1 and T2 when whole system is going upwards with acceleration = 2 m s^-2 (use g = 9.8 m s^-2).

[NCERT Exemp. Q. 5.28, Page 34]

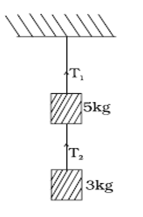
Solution:

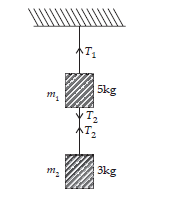
Acceleration of the system a= 2 m/s²   upward

For m₂ i.e. the 3 kg block:

T₂ – m₂g= m₂a
T₂ = m₂(a+g)=3(2+9.8) = 35.4 N

For m₁ i.e. the 5 kg block
T₁-T₂– m₁g= m₁a
T1 = T2 + m1(g+a)= 35.4 + 5(9.8 + 2) = 35.4 + 59 = 94.4 N

NCERT solutions for class 11 physics chapter 5 laws of motion

7) Block A of weight 100 N rests on a frictionless inclined plane of slope angle 30° (Fig. 5.7). A flexible cord attached to A passes over a frictionless pulley and is connected to block B of weight W. Find the weight W for which the system is in equilibrium.

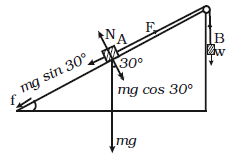
[NCERT Exemp. Q. 5.29, Page 35]

Solution:
mg =100 N

For A to be at rest,
mg sin30 = F
so, (1/2)mg = F
=> F = 0.5 x 100 N=50 N

For B to be at rest,
W = F = 50 N.

NCERT solutions for class 11 physics chapter 5 laws of motion

8) A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, calculate the minimum force required to be applied by the finger to hold the block against the wall?

[NCERT Exemp. Q. 5.30, Page 35]

Let F force is applied by finger on a body of mass M,

Under Balanced condition,
F = N The normal reaction of the wall on the book.

The minimum upward frictional force needed to ensure that the block does not fall is Mg.

The frictional force = μN

Thus, the minimum value of F=Mg/μ

9) Figure below shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions. If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle. [NCERT Exemp. Q. 5.32]

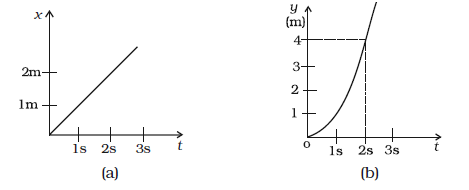
Solution:

[Fig (a) shows motion along the x-axis and from the graph, we can see that it’s uniform motion. (uniform velocity along the x-axis)]

Mass of the particle= 0.5 kg

We can get the velocity along x axis = Vx = dx/dt = slope of the line in (a) = 2/2 =1 m/s   [ in 2 secs it moves 2 m, used this as dt and dx respectively]

Acceleration along x axis = ax= dVx/dt = 0  [ this we have already said seeing the graph]

Force along x axis = Fx = m ax = 0

From figure b, it’s evident that y=t2   [in 2 secs it moves 4 m along y-axis ]

Velocity along y axis = Vy = dy/dt= 2t

Acceleration along y axis = dVy/dt=2

Force along y axis = Fy = m ay = 0.5 x 2 N = 1 Newton

As there is no component of force along the x-axis, and the entire force is found along the y-axis, so the net force is 1 N along the y-axis.

NCERT class 11 physics chapter 5 exercise solutions

10) A monkey of mass 40 kg climbs on a rope (figure) which can stand a maximum tension of 600 N. In which of the following cases will the rope break: the monkey

(a) climbs up with an acceleration of 6 ms–2
(b) climbs down with an acceleration of 4 ms–2
(c) climbs up with a uniform speed of 5 ms–1
(d) falls down the rope nearly freely under gravity?
(Ignore the mass of the rope).
NCERT Text Ex 5.33

cbse class 11 physics chapter 5 ncert solutions

Solution:
Maximum tension that the rope can bear, T max = 600 N
Mass of the monkey= m = 40 kg
g= 10 m/s²

Case (a)

Acceleration of the monkey, a = 6 m/s^2 upward.

Using Newton’s second law of motion, we can write the equation of net force as:
T – mg = ma
∴ T = m( g + a)= 40(10 + 6)= 640 N
As T >T max, the rope will break in this case.
Case (b)
Acceleration of the monkey, a = 4 m / s^2 downward
Using Newton’s second law of motion, we can
write the equation of net force as:
mg – T = ma
∴ T = m(g- a)= 40(10 – 4)= 240 N
As T < T max, the rope will not break in this case.

ncert class 11 physics chapter 5 exercise solutions

Case (c) The monkey here is climbing with a uniform speed of 5 m/s. So, its acceleration is zero. a = 0.
Using Newton’s second law of motion, we can write the equation of net force as: T – mg = ma
T – mg = 0
∴ T = mg= 40 x 10= 400 N
As T < Tmax, the rope will not break in this case.
Case (d)
When the monkey falls freely under gravity,
its acceleration will become equal to the acceleration due to gravity.
here, a = g
Using Newton’s second law of motion, we can write the equation of net force as
mg – T = mg
∴ T=m( g – g) = 0
As T < T max, the rope will not break in this case.