How to solve leaning ladder equilibrium numerical?
In this post, we will solve a numerical problem based on the equilibrium of a leaning ladder.
To do this you need to first understand the conditions of equilibrium. If you require some revision then you can quickly go through our physics tutorial on the equilibrium conditions first, before attempting this numerical.
Anyways, let’s begin solving the numerical.
Leaning ladder equilibrium numerical
Problem statement:
The ground is rough
A uniform ladder of length l rests against a smooth, vertical wall (Fig. 1).
The mass of the ladder is m, and the coefficient of static friction between the ladder and the ground is μs=0.40.
Find the minimum angle θmin at which the ladder does not slip.
How to solve this kind of problem:
In this post, we will understand this problem first and then take a step-by-step approach to solve the numerical.
Conceptualize Think about any ladders you have climbed. Remember that a large friction force between the bottom of the ladder and the surface is required to keep the leaning ladder in a balanced condition.
If the friction force is zero, then the ladder won’t be able to stay up. You may simulate a ladder with a ruler leaning against a vertical surface. You will find that the ruler slips at some angles and stay up at others.
Categorize We do not wish the ladder to slip, so we model it as a rigid object in equilibrium.
Analyze The free-body diagram (FBD) showing all the external forces acting on the ladder is illustrated in Figure 2.
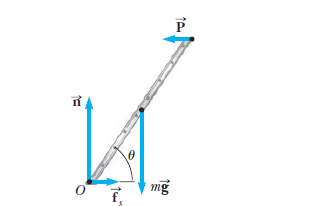
The force exerted by the ground on the ladder is the vector sum of a normal force n and the force of static friction fs.
The force P exerted by the wall on the ladder is horizontal because the wall is frictionless.
Apply the first condition for equilibrium to the ladder:
ΣFx= fs – P = 0 ……… (1)
ΣFy= n – mg = 0 ….. (2)
Solve Equation (1) for P:
P = fs ………(3)
Solve Equation (2) for n:
n = mg ……..(4)
When the ladder is on the verge of slipping, the force of static friction must have its maximum value, which is given by fs,max = μs n.
Combine this equation with Equations (3) and (4):
P = fs= μs n = μs mg …………. (5)
Apply the second condition for equilibrium to the ladder, taking torques about an axis through O:
Σ τ = P l sin θmin – mg (l/2) cos θmin = 0
Solve for tan θmin :
sin θmin / cos θmin = tan θmin = mg/ (2P) = mg/(2 μs mg) = 1/(2 μs) = 1/(2 x 0.4) = 1.25
hence, θmin= tan-1(1.25) = 51 °
Observation Notice that the angle depends only on the coefficient of friction, not on the mass or length of the ladder.
