Newton’s Second Law and equation of Force

Last updated on November 18th, 2021 at 01:26 pm

Newton’s Second Law states that the rate of change of momentum of a body is directly proportional to the net force applied on it, and this change in momentum takes place in the direction of the applied force.

Mathematically it can be stated this way: F∝ (mV-mU)/t. Here, F is the net force acting on the body of mass m for a time duration of t. U and V respectively are the initial and final velocities of the body. Let’s see how from this expression we get the equation of force as well.

So it’s evident that the second law of Newton was stated in terms of rate of change of momentum. When Newton’s first law gives us the concept of force, the second law of motion gives us the equation of force.

This equation is actually a formula to calculate the magnitude of force. With the help of this, we can calculate the magnitude of force applied, provided we know the mass of the object and its acceleration.

Also read: Application of Newton’s second law to find contact-forces between adjacent blocks

---

Newton’s second law and its mathematical representation

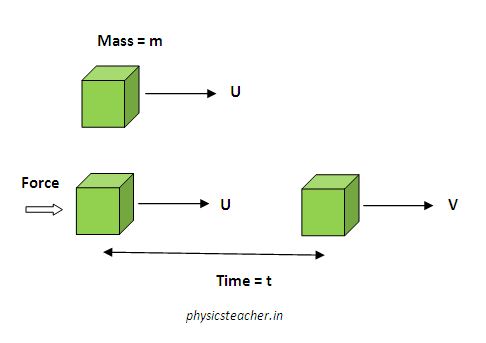
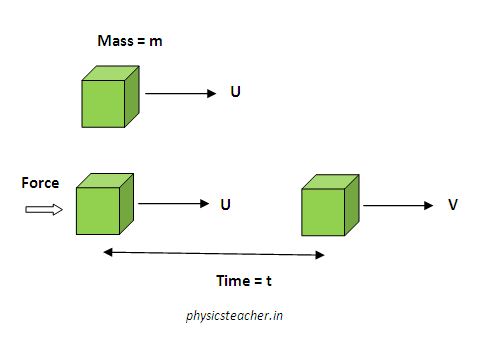
Referring to the above diagram: Here, U is the initial velocity of the object with mass m.  F_net is the magnitude of the net force being applied on that object for a time duration t. After time t the velocity of that object becomes V.

Initial momentum = mU and final momentum = mV.

So change of momentum = mV – mU

And rate of change of momentum = (mV – mU) / t

So as per Newton’s 2nd law,

F_net ∝ (mV – mU) / t

or,  F_net= k m (V – U) / t = k m a

Here, k is a constant.
and acceleration a = rate of change of velocity = (V – U) / t

so,   F_net = k m a……………..(1)

When unit force is applied on an object of unit mass and creates unit acceleration (i.e. when F =1, m=1 and a=1) then we get this equation,
F=kma
1=k.1.1
=>k=1

Putting this value of k in equation 1, we get

F = 1. ma = m a

i.e., Net Force  = mass X acceleration

Thus we get the equation of Force from Newton’s 2^nd Law of motion. This helps us in the measurement of force.

Equation of force

The equation of Force from Newton’s 2^nd Law of motion can be stated like this:

F = m a, where F is the force applied on a mass m producing an acceleration a.

Newton’s 2nd law – a few words

1.
Net force means unbalanced force. There may be multiple force components working simultaneously on a body. Few of them may cancel each other.

After getting the vector summation of all force components if we get a non-zero resultant force then we can say that a net force is working on the body.

2.
The net force causes the acceleration of the body. Acceleration means a change in velocity with time.

3.
If force is zero, then from F =ma we get ma = 0
As m is non-zero, so acceleration a = 0.
So in the absence of force, there is no acceleration.

---

The first law of motion from Newton’s second law of motion

From the last paragraph above we have seen that if the net force is zero, then from the equation F =ma we get ma = 0
As m is non-zero, we can say that acceleration a = 0.
To summarize, in the absence of net force, there is no acceleration.

Again when acceleration is zero that means no change in velocity.
– That means the object in motion moves with a uniform velocity when the net force on it is zero.
– Similarly, a static body remains static when the net external force on it is zero.
This is basically the statement of Newton’s first law of motion.
Now, we will solve a few numerical problems now, in the next paragraph.

---

Newton’s 2nd law – sample problems

1) Force of 1000 Newton is applied on a 25 kg mass for 4 seconds. What would be its velocity?

 Solution:

F =1000 N
m=25kg
t= 4 sec
u=0
v=?

Acceleration = a = F/m = 1000/25 = 40 m/s² 

v = u + at =0 + 40X4 = 160 m/s

2) A force is applied on a mass of 20 kg for 3 seconds. As the force is removed the mass moves 81 meter in 3 seconds. What was the value of the force applied?

Solution:

In the first 3 secs when the Force is present the body moves with acceleration and attains a velocity. After these first 3 seconds, the force is removed. And in the next 3 secs when Force is not there, the body moves with a uniform velocity.

From the data we can find the uniform velocity for the next 3 secs:
V = 81/3 = 27 m/s

This velocity was attained in the first 3 seconds when the force was present and the mass was moving with acceleration.

So we can calculate the acceleration in the first 3 seconds. a = (27-0)/3 = 9 m/s².

Therefore the force applied on the mass for first 3 secs= mass x acceleration = 20 x 9 = 180 N

Contact forces between 2 blocks: Analysis using Newton’s Laws

Read the full article here: Contact forces between 2 blocks: Analysis using Newton’s Laws

Related Posts

third law of motion