Gravitation class 11

Last updated on July 27th, 2023 at 10:01 am

This post provides study material on Gravitation class 11 [Physics Chapter 8 CBSE] in a nutshell. These gravitation class 11 Notes & formulas summarize the key concepts, equations, and applications. It also lists down a set of selected questions (prepared for ISC, CBSE class 11 physics, grade 12 physics, and UPSC preparation, IAS exams).

Isaac Newton unified “earthly” bodies and “heavenly” bodies with the Universal Law of Gravitation. Newton used the universal law of gravity to prove that the moon is accelerating towards Earth just as a body on Earth is falling towards Earth. The acceleration of both the moon and the object on Earth is calculated using the same formula.

The force of attraction between any two bodies in the universe is called gravitation.
The force of gravitation is the weakest force in nature. However, it is the most important force in the universe because it plays an important role in planetary motion, the birth of a star, etc.

Table Of Contents

Gravitation class 11 [Notes & Formulas]

Gravitation class 11 [Notes & Formulas]

The subtopics are covered in the following paragraphs.

Newton’s Law of Gravitation

Newton’s Law of Gravitation: The gravitational force of attraction between any two bodies in the universe is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Importance of this law: Newton’s law of gravitation explains the rotation of the moon around the earth or the rotation of the earth around the sun. It correctly predicts the solar and lunar eclipses and the orbits and time periods of modern artificial satellites. The cause behind the tides in the oceans is mainly the gravitational force of attraction between the moon and ocean water.

Gravity and g

Gravity is the force of attraction exerted by the earth towards its center on a body lying on or near the surface of the earth. It is called the earth’s gravitational pull. Thus, gravity is a special case of gravitation.

The force of gravity acting on a body is the measure of the weight of the body. The force of gravity produces acceleration in a body and it is known as acceleration due to gravity. It is denoted by ‘g’.

If a body is of mass ‘m’, then its weight at the surface of the earth is mg.
Weight = mass × acceleration due to gravity.
W=mg

The acceleration due to gravity g decreases above and below the earth’s surface. Hence, the weight of a body decreases with an increase in height above the earth’s surface or an increase in depth below the earth’s surface.

The value of ‘g’ is maximum at the poles and minimum at the equator of the earth. At the center of the earth, ‘g’ is zero.

Formulas of The Universal Law of Gravity

1) From the law of gravitation we get this equation: F_G = Gm₁m₂ / r² ;

This equation presents the force of gravity between an object with mass m₁ and another object of mass m₂ and a distance between them of r.

2) G = 6.67 x 10^-11 N m² / Kg² ; G is the universal constant of gravity;

3) g = Gm/ r²; This is the formula for the gravitational field strength or gravitational acceleration (or Acceleration due to gravity) of a planet with mass m and radius r. Note that this is not really a separate equation but comes from Newton’s second law and the law of universal gravitation.

Acceleration due to gravity is independent of the mass, shape, size, etc. of a falling body i.e. light and a heavy freely falling body will attain an equal acceleration which is equal to the acceleration due to gravity (g). The average value of ‘g’ at the surface of the earth is 9.8m/s^2.

The heavier a planet or satellite, the higher its ‘g’. The value of ‘g’ at the surface of the moon is 1/6th of the value at the earth’s surface. The value of acceleration due to gravity is minimum at the planet Mercury and maximum at planet Jupiter.

Satellite

The body revolving around a planet continuously in an orbit is called a satellite.
Moon is a natural satellite of the Earth.

Since 1957, many man-made satellites have been put in different orbitals around the earth. They are called Artificial Satellites.

A satellite revolves around the planet in an orbit under the effect of the centripetal force provided by the gravitational force of attraction between the satellite and the planet.

The minimum velocity with which a satellite is put into its orbit is called the orbit velocity or orbital velocity of the satellite which is expressed as per the following equation:

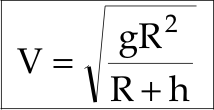
Here, V = orbital velocity, g = acceleration due to gravity, R = radius of the earth, & h = height of the satellite above the surface of the earth

If h<<< R i.e. for nearby orbit, we can consider that R+h = R
Hence, for nearby orbit, the orbital velocity equation for a satellite is: V = √(gR)

For the Earth, the orbital velocity of a satellite in a nearby orbit is 8 km/second and it is calculated as follows:

V = √(gR) = √(10 x 6400 x 1000) = 8000 m/s = 8 Km/ second. [Taking, g =10 m/s^2 and the Radius of the earth is taken as = R = 6400 Km ]

Learn more about the orbital velocity & derivation of its equations in our post on Orbital velocity derivations & concepts.

(i) Geostationary Satellite: It appears always at a fixed location above the earth in its orbit. Its time period of revolution around the earth is 24 hrs and its height is 36000 km above the equator of the earth. It rotates around the earth from west to east, similar to that of the earth.
Its speed is 3.1 kms/s. Its orbit is coplanar to the equatorial plane of the Earth. It is also known as a geosynchronous satellite.

(ii) Polar Satellite: It revolves around the earth in a polar orbit which is at 90° to the equatorial plane. It passes over both the north and south poles of the earth once per orbit. Hence, every location on earth lies with the observation of polar satellites twice each day. It is also known as the sun-synchronous satellite.
In order to monitor 100% of the earth’s surface, three geostationary satellites are required while a single polar satellite can do the same job.

Escape Velocity

The minimum velocity required to throw a body so that it becomes free from the earth’s gravitational pull is called escape velocity. It is given as V = √(2gR) = 11.2 km/s for the earth where g is the acceleration due to gravity and R, is the radius of the earth.

Learn more about the Escape velocity & derivation of its equation in our post on Escape Velocity & derivation of its equation

Effect of gravity on the weight of the body

When a body falls freely, its weight becomes zero. This situation is known as weightlessness. In a spacecraft or satellite, the effective weight of a body is zero because the gravitational force is balanced by the centrifugal force.

When a lift is at rest or is moving up/ down with a uniform velocity, the weight of the body inside it remains unchanged.
But, when the lift accelerates upwards, the weight of a body in it increases while downwards the weight of a body decreases.

Kepler’s laws of planetary motion

(i) The First Law: Every planet revolves around the sun in an elliptical orbit.
(ii) The Second Law: The average radius of the elliptical orbit of the planet sweeps out equal areas in equal intervals of time.
(iii) The Third Law: The square of the time period of revolution of a planet is directly proportional to the cube of the average radius of its elliptical orbit.

Learn More about Kepler’s third law derivation here.

Class 11 Gravitation – Key concepts

When using the Universal Law of Gravity formula and the constant G above, make sure to use units of meters and kilograms.
Newton invented calculus in order to prove that for a spherical object (like Earth) one can assume all of its mass is at the center of the sphere (thus in his formula, one can use the radius of Earth for the distance between a falling rock and Earth).
An orbital period, T, is the time it takes to make one complete rotation.
If a particle travels a distance 2πr in an amount of time T, then its speed is the distance over time or 2πr/T.
Planets revolve around the sun in elliptical orbits with the sun at one of the foci.
The gravitational force is much smaller than the electrical force because the value of G is very small.
Gravitation is a conservative force.
Gravitation is a central force.
G is a scalar quantity.
Work done in moving unit mass from infinity to any point in space is called gravitational potential at that point.
Gravitational potential is a scalar quantity.
Gravitational potential due to the earth at its surface is given by: Ve = – GMe|Re where Me = mass of the earth and Re = radius of the earth.
The unit of gravitational potential is J/kg.
The gravitational intensity inside a hollow spherical shell is zero.
Variation of g inside the earth is linear. That is, it increases in direct proportion to the distance from the center of the earth.
A decrease in acceleration due to gravity at a depth d is given by: gd/R, where R = radius of the earth.
Orbital velocity very near the surface of the earth is 7.92 km/s.
The greater the height of the satellite smaller the orbital velocity.
The time period of the satellite very near the surface of the earth is about 84.6 minutes.

Gravitation – Key Applications

To find the speed of a planet or satellite in an orbit, realize that the force of gravity is the centripetal force. So set the force of gravity equal to mv²/r, where v is the speed of the planet, m is the mass of the planet or satellite, and r is the distance of the planet to the sun or the satellite to the Earth.
The Geo-synchronous orbit is an orbit in which the satellite takes the same amount of time to orbit the planet as the planet takes to make one revolution. For satellites to be over the same place on the planet at all times, they must be in a Geo-synchronous orbit.

Gravitation class 11 Questions

This data set is required to answer the following questions
[The Earth-Moon distance is about 3.8 x 10^8 m
The Earth-Sun distance is about 1.5 x 10^11 m
The mass of the Sun is about 2×10^30 kg
The mass of the Earth is about 6×10^24 kg
The radius of the Earth is 6.4X10^6 m]

Which is greater – the gravitational force that the Earth exerts on the moon, or the force the moon exerts on the Earth? Why doesn’t the moon fall into the earth?
Which is greater – the gravitational force that the Sun exerts on the moon, or the force the Earth exerts on the moon? Does the moon orbit the Earth or the Sun? Explain.
Suppose you’re standing in an elevator on a bathroom scale(weighing machine). Draw an FBD for you and label the two forces acting on you. Describe how the scale reading compares to your weight when
- The elevator is at rest
- The elevator is moving up at a constant speed
- The elevator is accelerating upward
- The cable breaks and the elevator is in free fall
Astronauts in orbit are not beyond the pull of earth’s gravity – in fact, gravity is what KEEPS them in orbit! So why are they “weightless”? Explain briefly.
Use Newton’s Law of Universal Gravitation to explain why even though Jupiter has 300 times the mass of the earth, on the “surface” of Jupiter you’d weigh only 3 times what you weigh on earth. What other factor has to be considered here?
Calculate the force of gravity between two human beings, assuming that each has a mass of 80 kg and that they are standing 1 m apart. Is this a large force?
What is the force of gravity between an electron and a proton? Do you think this is what keeps the electron ‘orbiting’ the proton in the hydrogen atom?
At what height above the earth would a 400-kg weather satellite have to orbit in order to experience a gravitational force half as strong as that on the surface of the earth?
The Moon’s period around the earth is 27.3 days and the distance from the earth to the moon is 3.84 x 10^8 m. Using this information, calculate the mass of the Earth. (note: this calculation assumes a circular orbit. Is your answer high or low? Why?).

Universal Gravitation Law & derivation of the gravitational force equation	Relation between G and g	Geostationary satellite
Gravitational field strength on the earth	Gravitational potential energy	value of g
Gravitational field strength formula & definition	How to measure G	g near moon
Orbital velocity	Escape Velocity	Kepler’s third law