Harder Numerical problems based on SNELL’S LAW – in Light chapter physics

Last updated on July 4th, 2023 at 03:02 pm

Here we have a set of numerical problems based on Snell’s Law from the chapter ‘Light‘ of fundamental physics. This numerical set is a bit harder to solve but certainly will be helpful to strengthen your concepts on Snell’s Law.
Read about this law and its formula here: our post on Snell’s Law

Harder Set of Numerical problems based on SNELL’S LAW (Chapter Light)

Problem #1 )

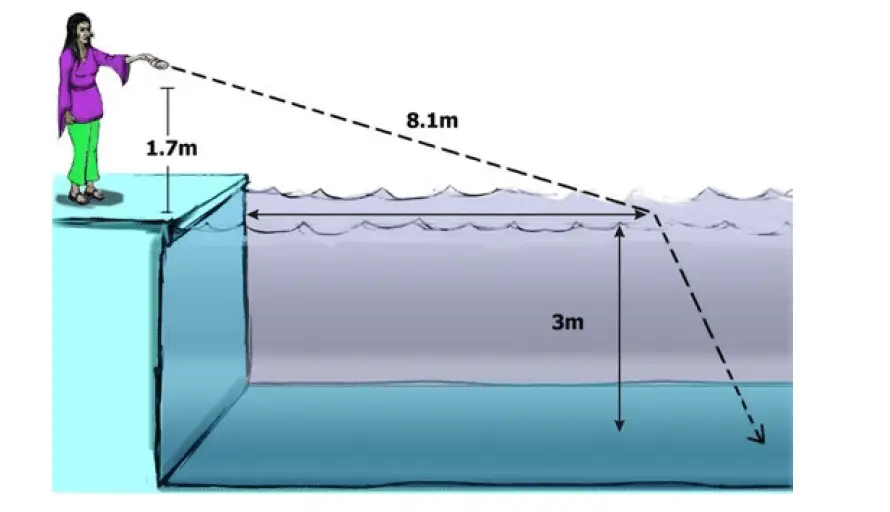
Diana stands at the edge of an aquarium 3.0 m deep. She shines a laser at a height of 1.7 m that hits the water of the pool 8.1 m from the edge.

1. Draw a diagram of this situation. Label all known lengths.
   
2. How far from the edge of the pool will the light hit bottom?
   
3. If her friend, Walker, were at the bottom and shined a light back, hitting the same spot as Diana’s, how far from the edge would he have to be so that the light never leaves the water?

Problem #2)

A light source sits in a tank of water, as shown.

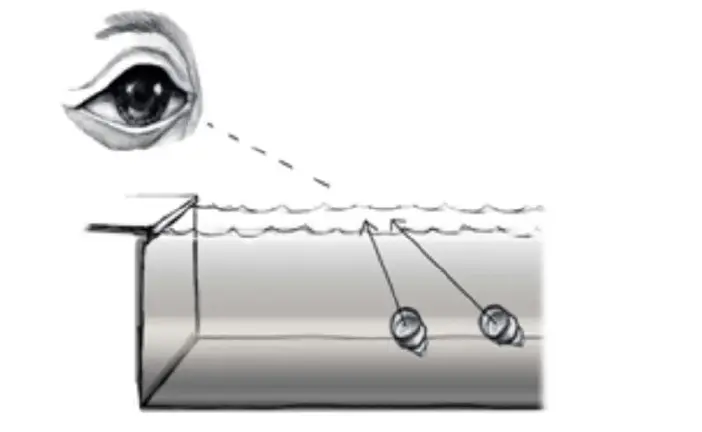
1. If one of the light rays coming from inside the tank of water hits the surface at 35 degrees, as measured from the normal to the surface, at what angle will it enter the air?
   
2. Now suppose the incident angle in the water is 80 degrees as measured from the normal. What is the refracted angle? What problem arises?
   
3. Find the critical angle for the water-air interface. This is the incident angle that corresponds to the largest possible refracted angle, 90 degrees.

Solutions:

Try to attempt and solve the numerical problems given above. Read about this law and its formula here: our post on Snell’s Law