Orbital Velocity derivation & concepts for class 11 | How to derive the orbital velocity equation?

Last updated on August 31st, 2021 at 10:53 am

In this post, we will focus on the Orbital Velocity derivation to come up with orbital velocity formula sets (covering class 11 syllabus). This derivation is equally applicable to the planets revolving around the Sun in their orbits and the satellites revolving around their specific planet. We will also discuss the concepts and definition of Orbital Velocity.

The basic principle that is leveraged while going for this derivation is that the centripetal force required for the circular motion is supplied by the gravitational force acting between the revolving body and the central body (the entity at the center of the circular orbit)

---

Orbital Velocity Derivation | How to derive the orbital velocity equation?

First, we will derive the Orbital velocity expressions or equations (2 sets) and later will derive the Orbital Velocity for a nearby orbit. (so you get total 3 sets of equations)

1) Orbital Velocity Formula derivation – set 1 (for class 11)

The Gravitational Force between the earth and the satellite = F_g = (G.M.m)/r²  ……………… (1)

G is the Gravitational Constant.

The centripetal force acting on the satellite = F_c = mV²/r    ……………………….. (2)

Here, M is the mass of the earth and m is the mass of the satellite which is having a uniform circular motion in a circular track of radius r around the earth.

V is the linear velocity of the satellite at a point on its circular track.

Now, this r is the sum of the radius of the earth(R) and the height(h) of the satellite from the surface of the earth.

r = R + h

Now equating, equations 1 and 2 we get,

F_g = F_c

=>  (G.M.m)/r² = mV²/r 

V =√[(GM)/r]…………(3)

This is the first equation or formula of the Orbital Velocity of a satellite.

Here r = R+h

2) The formula of Orbital Velocity – set 2 (for class 11 – step by step derivation)

For a mass of m on earth’s surface, the following is true:

mg = (GMm)/R² ………………………. (4) 

Note, on earth surface h=0 and r = R. And gravitational force on a mass is equal to its weight on the surface.

From equation 4 we get this equation, GM = g. R² …………………….. (5)

Substituting this expression of GM in equation 3, we get,

V = [(gR²)/r]^1/2

 V =R . √(g/r) ……. (6)

This is the second formula. 

Here, as said earlier,
r = R +h

Next, we will derive the 3rd equation and that is for a NEARBY ORBIT, i.e. for an orbit that has a negligible height above the earth’s surface.

---

3) Orbital Formula derivation for Near Orbit

Let’s consider an orbit that is pretty close to the earth.

Now if the height of the satellite (h) from the surface of the earth is negligible with respect to the Radius of the earth, then we can write r=R+h = R  (as height h is negligible).

**From equation 3 (the fundamental form of orbital velocity equation), we get an equation of nearby orbit’s Orb. velocity:

V = √[(GM)/R] ………….(3.1)

**And from equation 6 we get another form of the equation for orbital speed (when height h is negligible) at near-earth orbit:

V_orbital = R . (g/r)^1/2

= R . (g/R)^1/2

V_orbital =√(gR) ……….(6.1)

here, R = r

---

Orbital Velocity formula class 11 – list of Orbital Velocity equations we derived

Here you get a few sets of Orbital Velocity expressions that are derived in this post. (covering class 11 Physics syllabus)

V_orbital = √[(GM)/r]
where G is the Gravitational Constant.
M is the mass of the earth.
And, r is the sum of the radius of the earth (R) and the height (h) of the satellite from the surface of the earth.
=> r = R + h

V_orbital = R . √(g/r)
Here, R = radius of the earth,
g = acceleration due to gravity
r =R + h

---

And for Nearby Orbit
(here, r = R as height (h) of the satellite from the surface of the earth is negligible)

V_orbital =√[(GM)/R]
where G is the Gravitational Constant.
M is the mass of the earth.
R = radius of the earth

 V_orbital =  √(gR)
where g = acceleration due to gravity,
R = radius of the earth

---

Orbital Velocity Definition

Orbital Velocity is the minimum velocity an object or particle has to maintain to continue its circular motion in its orbit.

In other words, it is the minimum velocity of the object in a circular motion that generates enough centripetal force to keep it in the circular orbit of a given radius.

---

Orbital Velocity and Centripetal force

We know for a circular motion to continue, a force called centripetal force is required to work upon the object in a circular motion.
And this force is real and acts towards the center of the circle. As this is a real force it’s to be supplied by a real mechanism or system.
A satellite of the earth moves in a circular track and the centripetal force acting on it is supplied by the gravitational force acting between the earth and the satellite.

Thus, a satellite maintains its own orbital velocity (or orbital speed – we use this term as well) when it revolves around a planet. Similarly, a solar planet does maintain its own required orbital velocity while revolving around the sun. In this case, the required centripetal force is supplied by the gravitational force acting between the planet and the sun.

---

How Orbital Velocity depends on the Radius of the orbit?

From the equations of Orbital Velocity, it’s evident that as the radius of the circular path increases, the minimum velocity requirement of the satellite to maintain its circular track decreases.

In other words, if the satellite rotates closer to the earth, it has to move faster. As the radius of the orbit increases, this velocity in orbit becomes less.

Interesting points:

If the radius of satellite orbit is made N times of the radius of the earth then its orbital velocity would be (1/N)^(1/2) times of the near-earth orbit orbital velocity.

If 2 satellites with radii r1 and r2 are orbiting in circular orbits, then the ratio of their velocities is v1/v2 = (r2/r1)^(1/2), where v1 and v2 are orbital velocities.

---

How Orbital speed depends on the mass of the satellite?

This velocity in an orbit doesn’t depend on the mass of the satellite.

---

Sample Numerical Problems with solutions (uses Orbital speed formula)

Q 1 ) Compare the orbital speed of satellites that have stable orbits with an altitude of 300 km:
(a) Above the Earth. (mass of earth = 6.0 × 10^24 kg, Radius of earth = 6370 Km)
(b) Above the Moon’s surface. (mass of moon = 7.4 × 10^22 kg; radius = 1700 km)

Solution: We will use this formula of orbital speed to solve this numerical.
V_orbital = [(GM)/r]^1/2

(a) For earth,

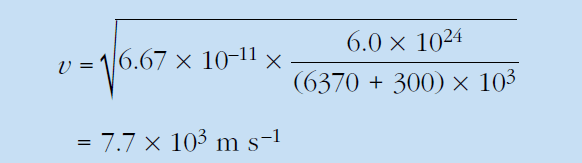
(b) for moon

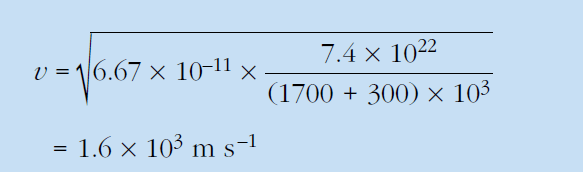
Q 2) Assume that a satellite orbits Earth 225 km above its surface. Given that the mass of Earth is 5.97 x 10²⁴ kg and the radius of Earth is 6.38×10⁶ m, what is the satellite’s orbital speed?

 Solution:
h =2.25×10⁵ m (height of the satellite’s orbit)
r_E =6.38×10⁶ m (Earth’s radius)
m_E =5.97×10²⁴ kg (Earth’s mass)
G = 6.67×10^-11 Nm^2/kg^2
Orbital velocity = V =?

We get the orbital radius r by adding the height of the satellite’s orbit to Earth’s radius.
r =h +r_E =2.25×10⁵ m + 6.38×10⁶ m = 6.61×10⁶ m

So, Orbital speed.
V = √[(G m_E)/r] = [G m_E)/r ]^1/2  = 7.76 x 10³ m/s

Related study- highly suggested for you:

We can use the equations of Orbital velocity to derive Kepler’s third law.
Here are some posts we would like to suggest for your further study.

1) Read the Post here for Kepler’s 3rd Law.
2) Also, here is another related & important article for you: Escape Velocity.
3) You may also go through this comprehensive class 11 physics notes on Gravitation topics.