Universal Law of Gravitation & Derivation of Gravitational Force formula

Last updated on June 5th, 2023 at 12:52 pm

The objective of this post is the study the Universal Law of Gravitation and the derivation of the Gravitational Force formula from the Universal Law of Gravitation.

Universal Law Gravitation by Newton states about a force of attraction between any two objects.
And as per this law, this force is (i) inversely proportional to the square of the distance between the objects and (ii) directly proportional to the product of the masses of these two objects involved.

State the Universal Law of Gravitation

Law of Gravitation or Law of Universal Gravitation by Newton states that “Every object in this universe is attracting every other object towards it with a force called the gravitational force of attraction. This force of attraction is (i) inversely proportional to the square of the distance between the objects and (ii) directly proportional to the product of the masses of these two objects involved.“

The universal gravitation equation thus takes the form
F_G ∞ m1.m2/ r²
=>F_G = G m1.m2/ r²

Direction of the gravitational force

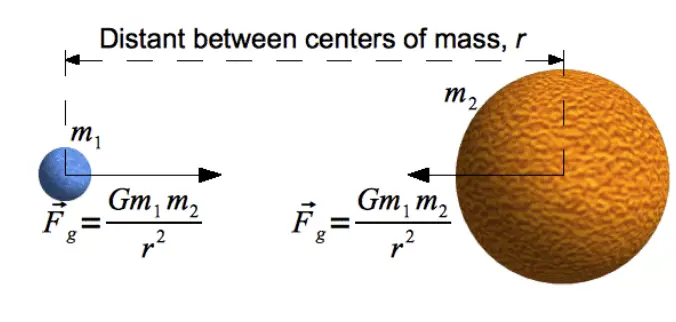
This force acts along the line joining the two objects. The object with mass m1 will apply this force on m2 and the direction of the line of this force will be from m2 towards m1.

The object with mass m2 will apply a force of the same magnitude on m1 and the direction of the line of this force will be just opposite i.e it would be from m1 towards m2.

Derivation of Gravitational Force formula | derivation of Universal Law of gravitation formula

Now we will derive the formula of the Gravitational force from the universal law of Gravitation stated by Newton.

Say FG is the magnitude of the force of gravitational attraction between any two objects, m1 is the mass of one object, m2 is the mass of a second object, and r is the distance between the centers of the two objects. (Objects are assumed to be spherical.)

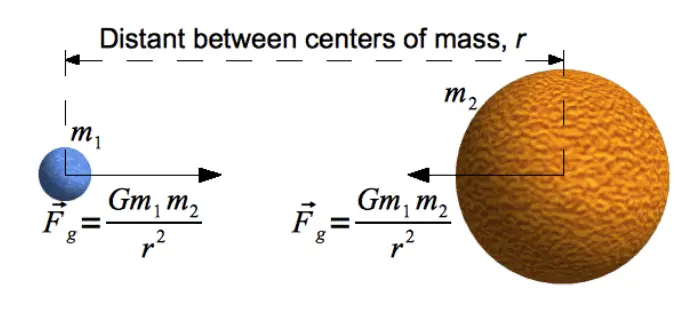
Now as said in the Law of Gravitation:

F_G ∞ m1.m2

and

        F_G ∞  1/r²

So,   F_G ∞ m1.m2/ r²

Thus the mathematical representation of the Universal Law of Gravitation results in the Derivation of the Gravitational Force formula which is summed up next.

The Universal law of gravitation can be summed by this gravitational force formula:   
F_G = (G.m1.m2)/r², where G is a constant that is known as Universal Gravitational Constant or Gravitational constant. This equation gives us the expression of the gravitational force.

**Also Read: Numerical Problems Based on Law of Gravitation

Universal Gravitational Constant or Gravitational constant – value, unit

In the equation of gravitational force, G is a constant, called Universal Gravitational Constant or Gravitational constant.

Its unit is Nm²kg^-2

And the Value of G (Gravitational constant): 6.67408 × 10^-11 Nm²kg^-2

**Also read: How to measure G (Universal Gravity Constant)

Law of Gravitation – Notes

With the law of universal gravitation, it is important to notice that two equal but opposite forces are present between any 2 objects. Earth pulls on the Moon and the Moon pulls on Earth with a force of equal magnitude.

On the Earth’s surface, Earth pulls down on a 1 kg mass with a force of magnitude 9.8 N, and the 1 kg mass pulls upward on Earth with a force of a magnitude 9.8 N. (Ref: Newton’s third law of motion.)

Importance of Newton’s Universal Law of Gravitation

• It has explained how every object on Earth is bound to the Earth’s surface in spite of it rotating continuously.
• It explains the motion of the Satellites (e.g. moon) around planets (like Earth).
• The motion of the planets around the Sun is also explained by this Universal law.
• It helps us to find out the value of g (acceleration due to gravity) for the earth.
• It helps us to understand why g on Earth is different from g on the moon.

Gravity on the Earth’s Surface

On the surface of a planet – such as Earth – the r in the Universal Law of Gravitation is very close to the radius of the planet. A planet’s center of mass is approximately at its center (for a spherical planet with azimuthal symmetry of density this is exactly true).

In addition, we can safely ignore the increase in height off the surface of the Earth when we are calculating gravity on the Earth’s surface itself. So we can say with very good accuracy that for objects near the surface of the earth, the r in the formula is constant and equal to the earth’s radius. Here’s an illustration:

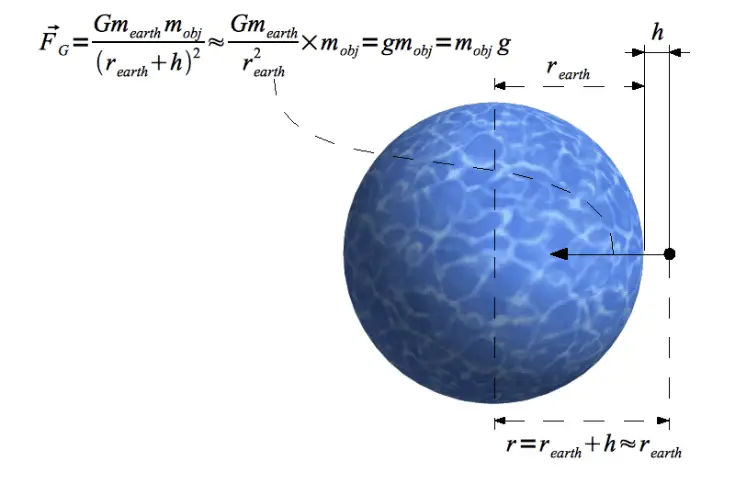
For any object a height h above the surface of the earth, the force of gravity may be expressed as:

Why don’t two people walking on the street get pulled toward each other due to a mutual gravitational attraction? – a case study

Solution
Consider the following: two people, one weighing 60 kg and the other weighing 80 kg, are separated by a distance of 5.0 m on the street. Let’s calculate the attraction force between them.
We have this equation, F = Gm1m2/r^2

Known quantities:
G = 6.67 × 10–11
m1 = 60 kg
m2 = 80 kg
r = 5.0 m

∴F =6.67 × 10–11 × 60 × 80/5^2
= 1.3 × 10–8 N Towards each other
The force between them is too small to have any effect, in fact, it is even too small to be detected in any usual manner.

Jupiter has saved Earth from being bombarded by many more asteroids

Jupiter has a mass of 1.9 × 10^27 kg. This is approximately 200 times the mass of Earth. Some astronomers believe that Jupiter has saved Earth from being bombarded by many more asteroids than it actually has in the past. Why is this?

Solution
Jupiter’s gravity can attract asteroids that stray too close to the planet, pulling them in and thus preventing them from continuing in an orbit that may pass close to Earth or collide with Earth.

Sample Numerical problems – solved

Q 1) Determine the magnitude of the gravitational attraction force between the Sun and the Earth, given that the mass of the Sun is 1.99 × 10^30 kg, the mass of the Earth is 6.0 × 10^24 kg and they are separated by 1.5 × 10^8 km as measured between their centers.
Solution
F = Gm1m2/r^2
m1 = 1.99 × 10^30 kg
m2 = 6.0 × 10^24 kg
G = 6.67 × 10–11
r = 1.5 × 10^11 m
∴F =(6.67 × 10–11)(1.99 × 10^30)(6.0 × 10^24)/(1.5 × 10^11)^2
= 3.54 × 10^22 N Attraction

Q 2) Two large asteroids, both with a mass of 1.5 × 10^9 kg, pass within 300 km of each other. What force of attraction would there be between the asteroids? Comment on: This result is equivalent to the weight of a small grain of sand!

Solution
F = Gm1m2/d^2
= 6.67 × 10–11 X1.5 × 10^9 X 1.5 × 10^9/(300 × 10^3)^2
= 1.7 × 10–3 N

Q 3) Tides on Earth are caused by a combination of the Moon’s and the Sun’s gravity acting on the oceans. Compare the strength of the Moon’s gravity on Earth’s surface (approximately 400 000 km from the Moon’s center) to that on the Moon’s surface. The radius of the Moon is 1700 km.
Solution
Newton’s law of universal gravitation is an example of the inverse square law: that is, the strength of the gravitational field is inversely proportional to the square of the distance, so:
The strength of gravity on the Moon’s surface is = (400000/1700 )^2 = 5.5 × 10^4 times greater than that exerted at Earth’s surface.

Now, why does a stone fall towards the earth but the earth doesn’t seem to run upwards towards it? Read here.

This post is apt for students who are looking for the universal law of gravitation derivation for class 9 and class 11/12 courses. [CBSE, ICSE, IGCSE, & Other International high school boards for science].

Related Posts for Further Study

Here are some related & relevant posts we would like to suggest for your further study.

1) Read the Post here for Kepler’s 3rd Law.
2) Also, here is another related & important article for you: Escape Velocity.
3) You may also go through this comprehensive class 11 physics notes on Gravitation topics.