Escape velocity Derivation & concept – derive formula √(2gR) for earth

Last updated on May 3rd, 2021 at 10:28 am

We will first understand what escape velocity is and then we will focus on the escape velocity derivation to get its formula or equation. Now, what is escape velocity?

---

---

Define Escape Velocity

Escape velocity is defined as the minimum velocity with which if an object is thrown from the surface of the earth or any other planet or satellite then the object defeats the gravitational attraction working on it and can go beyond this attraction. Escape velocity is the velocity at which an object is able to escape from the gravitational field of a planet.

---

Concepts of Escape Velocity – explanation with diagram

It has been seen that when the initial horizontal velocity of a projectile increases sufficiently, the object will not fall back to the Earth following a parabolic pathway, but will describe a circular path around the Earth (see Figure 1). If the velocity is increased further, an elliptical path will follow.

Eventually, with even greater horizontal speed, it will escape the Earth’s gravitational pull and never come back (see Fig. 1).
This velocity is referred to as the escape velocity of the Earth. Sir Isaac Newton is considered to have been the first to think about such a situation, launching a projectile horizontally from a very high tower.

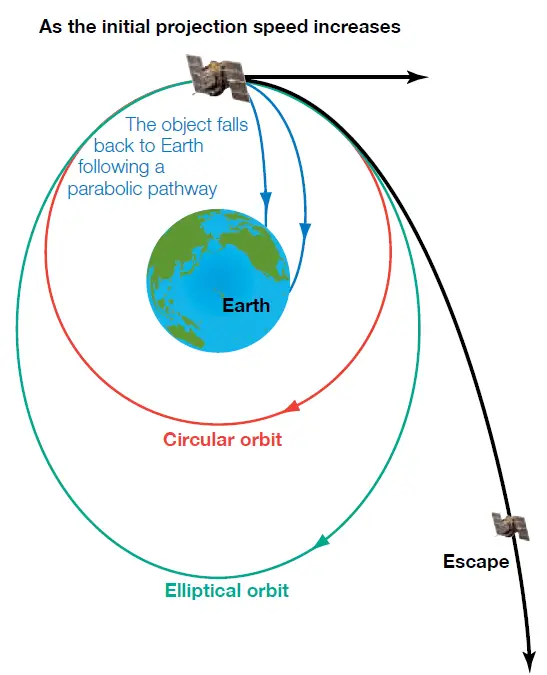
This is to be noted that this concept of escape velocity is not only applicable to the earth but also it is equally applicable to all other planets and satellites.

But the value of this velocity would be different for them. As we derive the formula of this escape velocity, this point will get clearer.

---

Escape velocity Derivation – derive formula as √(2gR)

We will derive the equations using the following condition:

The initial kinetic energy of the object would at least equalize the amount of work done to send the same object from the surface of the earth to an infinite distance.

In other words, the kinetic energy (E_k) of the object due to its velocity (v) must exceed or at least equal its gravitational potential energy (E_p).

Therefore: E_k >= E_p ………………. (i)

Initial Kinetic Energy:

Now if the escape velocity of earth is V, then the initial kinetic energy(KE) of the object would be:
Kinetic Energy = E_k = (½) m V² ……………….. (ii)

Work Done to send the object from the surface of the earth to an infinite distance or Gravitational Potential Energy:

Gravitational Potential Energy = E_p= (GMm/R) …………. (iii)

Getting the expressions of escape velocity now by equalizing E_k and E_p:

From all the equations above, we get:

½ .m.V² = (GMm)/R

V² = (2GM)/R

Escape Velocity
V = √( 2GM/R) ………   [iv]

As the expression of the acceleration due to gravity on the earth’s surface is g = GM/R²
[for this equation read this: acceleration due to gravity]

i.e., g.R² = GM,
therefore we can rewrite equation number (iv) as follows:

V = √( 2GM/R) = ( 2GM/R) ^½ = [ (2 g R²) / R ]^(1/2) = (2gR)^(1/2) = √(2gR)

Escape Velocity
V=√(2gR)………… (v) 

As per the condition opted for the derivation, here are the equations for the minimum value of the escape velocity:
V = √( 2GM/R)
V= √(2gR)

Including the ‘greater than’ sign in the equations we get the final expressions of the escape velocity:
V >= √( 2GM/R)
V >= √(2gR)

---

Also Read: Gravitational Potential Energy – concepts and Derivation of the formula

---

Also Read: derivation of the kinetic energy equation

---

What factors affect the value of the escape velocity?

It’s to be noted that this escape velocity doesn’t depend on the mass of the object which is being thrown.

But this escape velocity certainly depends on the mass and the radius of the planet or satellite or the star from where the object is being thrown. (see equation iv above)

This has two consequences:

1. Different planets have different escape velocities.
2. A massive body, such as a rocket, will have the same escape velocity as a small object like an atom.

---

Escape Velocity is √2 times of Orbital velocity for nearby orbits

For an orbit that is pretty close to the earth, we can ignore the height above the surface and can consider only the radius of the earth as the distance between the satellite and the earth’s center. For this scenario, we get an equation for orbital speed

V_orbital =  √(gR) 
[ to find this derivation please refer to our post: Orbital Velocity ]

Whereas as found,  V_escape = √(2gR)

Very clearly it’s visible that the Escape velocity is √2 times of Orbital velocity for nearby orbits.

---

Value of the earth’s Escape Velocity

We know the value of g on the surface of the earth. It’s 9.8 m/s^2.

The radius of the earth (R) is 6400 Km = 6.4 X 10^6 meters.

So from these data, we get the escape velocity of the earth from equation (v) above:

Escape Velocity of earth =V =√(2gR) = √(2 X 9.8 X 6.4 X 10^6) m/s =11200 m/s =11.2 km/s = 7 mile/second

So if an object is thrown upwards with a velocity of 11.2 Km/Second from the earth’s surface, it will be able to escape i.e. go beyond the gravitational field of the earth.

---

Why, unlike Earth, Mercury does not have an atmosphere? | Escape Velocity for Mercury

We will calculate the escape velocity for Mercury and will find out why, unlike Earth, Mercury does not have an atmosphere.

Mass of Mercury M= 3.3 x 10^23 kg
Radius of Mercury R = 2439000 m
G = 6.67 x 10^(-11)
escape velocity V >= √( 2GM/R)
Putting the values in the equation and post calculation we get the escape velocity for Mercury as 4.2 Km/s

The escape velocity for Mercury as calculated above is quite small (compared to 11.2 km/s on Earth).
Since the escape velocity is independent of an object’s mass, under normal circumstances, the velocity of gas molecules can easily exceed the escape velocity of Mercury due to their own thermal energies, especially as Mercury is close to the Sun and therefore very hot.

Consequently, a small planet like Mercury will not be able to retain its atmosphere, as the majority of its atmospheric gas molecules will escape into space.

For the same reason, the Moon cannot retain its own atmosphere as any gas molecules will be able to move faster than the Moon’s escape velocity.

Escape Velocity for moon and Jupiter

Escape Value of the moon: 2.38 km/sec

and that of Jupiter: 59.5 km/sec

 Suggested Reading:

Orbital Velocity

Universal Law of Gravitation