Derivation of Gravitational potential energy equations

Last updated on June 14th, 2022 at 10:39 am

This post focuses on the Derivation of Gravitational potential energy equations when the reference varies from the planet’s surface to infinity. Gravitational potential energy, E_p, is the energy of a mass due to its position within a gravitational field. This energy can be released (and converted into kinetic energy) when the body is allowed to fall.

In this post, let’s find out the concepts & equations of Gravitational potential energy when the reference point varies from the planet’s surface to infinity. We will discuss & derive 2 equations: (1) E_p = mgh (2) E_p = – G m₁m₂ / r

Derivation of The gravitational potential energy equation – when the reference point is the surface of the earth

Gravitational potential energy E_p at some point x above the ground
= work done to move to the point x with the vertical height h from the ground
= force required × distance moved (since work W = Fr)
Gravitational potential energy E_p = (mg) × h = mgh

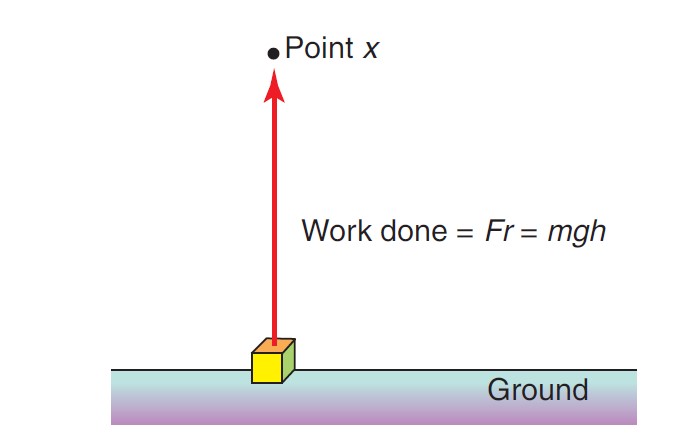
Hence, in this case, E_p = mgh. Here, We chose the ground as our starting point because this is our defined zero level; that is, the place where E_p = 0. Note that since work must be done on the object to lift it, it acquires energy.
Hence, at point x, E_p is greater than zero.

Derivation of the gravitational potential energy on a larger, planetary scale when reference point is at infinity

On a larger, planetary-scale we need to rethink our approach.

Due to the inverse square relationship in the Law of Universal Gravitation, the force of attraction between a planet and an object will drop to zero only at an infinite distance from the planet.

For this reason, we will now choose infinity (or some point a very large distance away) as our level of zero potential energy.

There is a strange result of our choice of zero level.

Because gravitation is a force of attraction, work must be done on the object to move it from a point, x, to infinity; that is, against the field so that it gains energy, Ep. That means, at infinity the potential energy becomes the largest.

Therefore, E_p at infinity > E_p at point x
but E_p at infinity = 0
so that E_p at point x < 0
that is, E_p at point x has a negative value! (see figure 2)

Hence we can say, If we choose a planet’s surface as the zero level, Gravitational Potential Energy E_p at x has a positive value. If infinity is chosen as the zero level, E_p has a negative value.

Using the same approach as earlier, the gravitational potential energy, E_p, of an object at a point, x, in a gravitational field is equal to the work done to move the object from the zero energy level at infinity (or some point very far away) to point x. It can be shown mathematically that: E_p = – force x distance = – (G m₁m₂ / r^2) x r = – G m₁m₂ / r, where m₁ is the mass of the planet, and m₂ is the mass of the object. r is the distance between the center of the planet and the object.

We have seen how gravitational potential energy E_p can be expressed as E_p = – G m₁m₂ / r

Why is the gravitational potential energy negative?

At a position very far away from Earth, an object would experience negligible gravitational attraction. The place at which gravity becomes zero is in fact an infinite distance away. By definition, any object at such a distance is said to have zero gravitational potential energy. If an object was then given a small ‘nudge’ or a push towards Earth, it would begin to fall towards Earth, losing gravitational potential energy as it gains kinetic energy. The more gravitational potential energy the object loses, the more negative the value of Ep (subtracting from zero results in a negative value).

Conversely, to reach this infinite distance from within the gravitational field, positive work has to be done on the object, that is, an effort is required to push the object upwards. So, if positive work is added to the object and the object ends up with a zero gravitational potential energy at an infinite point from the Earth, the object anywhere below that point must have negative energy.
Analogy: If you keep adding positive numbers to an unknown number, and end up with a zero, then you are quite certain that you started off with a negative number.

Change in gravitational potential energy (ΔEp) | formula of ΔEp

Although the gravitational potential energy is negative, the change in gravitational potential energy can be positive. The change in gravitational potential energy is equal to the second potential energy minus the first potential energy, or more correctly it is the less negative potential energy minus the more negative potential energy.
For two positions in the gravitational field with distances of r1 and r2 from the center of the Earth respectively, where r1 is greater than r2:

ΔEp = – GmM/r1 – (– GmM/r2 )
= (GmM/r2) ––(GmM/r1)
ΔEp = GmM ( 1/r2 – 1/r1 ) [ This is the formula of Change in gravitational potential energy or ΔEp ]

Since r1 is greater than r2, 1/r1 is less than 1/r2, therefore 1/r2–1/r1 is positive.
Consequently, ΔE is positive.

Numerical Problem solving using the formula of Change in gravitational potential energy or ΔEp

Calculate the change in gravitational potential energy for a scientific instrument with a mass of 150 kg, when it is moved from ground level to the top of Mount Everest, where the height is 8848 m.

Solution:

ΔEp = Ep at the top of Mount Everest – Ep at the surface of the Earth
ΔEp = –(6.67 × 10–11) × (6.0 × 10^24) × 150/(6378000 + 8848) – [–(6.67 × 10–11) × (6.0 × 10^24) × 150/6378000 ]
ΔEp =( (6.67 × 10–11) × (6.0 × 1024) × 150 × (–1/(6378000 + 8848)+1/6378000 )
ΔEp = 1.30 × 10^7 J
Or
ΔEp = 13 MJ

Gravitational potential energy equations | Summary

1] If we choose a planet’s surface as the zero level or reference, Gravitational Potential Energy E_p at x has a positive value.
If infinity is chosen as the zero level, E_p has a negative value.

2] Gravitational potential energy E_p = (mg) × h = mgh (if we choose a planet’s surface as the zero level or reference)

3] Gravitational potential energy E_p can be expressed as E_p = – G m₁m₂ / r (if infinity is chosen as the zero level)

Also Read: Law of gravitation & derivation of the formula for Gravitational force