How to measure universal gravitational constant | Measurement of G

Last updated on April 12th, 2021 at 11:55 am

Henry Cavendish first measured the universal gravitational constant G in 1798. The apparatus used is shown in Figure 1. Other experimenters repeated Cavendish’s measurement of G with various improvements and refinements. All measurements of G are found to be difficult because of the extreme weakness of the gravitational attraction.

Setup of Henry Cavendish to measure universal gravitational constant G

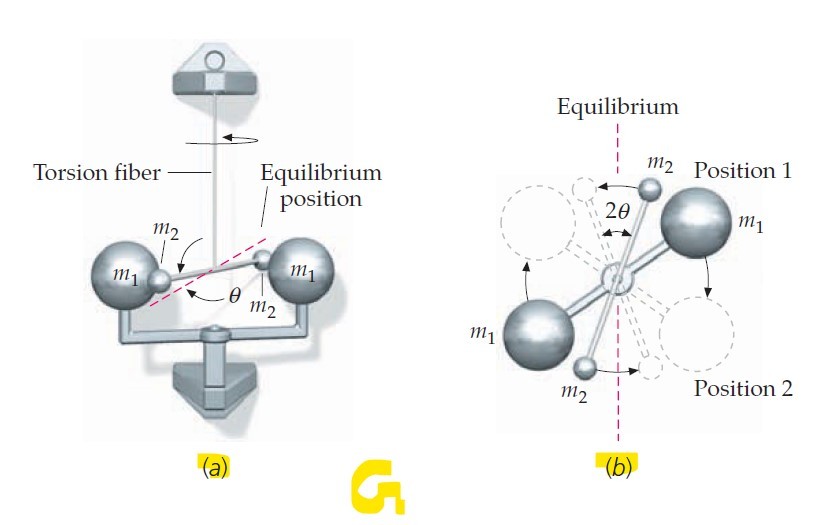
Experiment steps to measure G

(a) Two small spheres, each of mass m₂ are attached at the ends of a light rod. The rod is suspended by a fine fiber. Careful measurements determine the torque required to turn the fiber through a given angle.

Two large spheres, each of mass m₁ are then placed near the small spheres. Because of the gravitational attraction of the large spheres of mass m₁ for the small spheres, the fiber is twisted through a very small angle θ from its equilibrium position.

(b) Figure b shows the apparatus as seen from above. After the apparatus comes to rest, the positions of the large spheres are reversed, as shown by the dashed lines, so that they are at the same distance from the equilibrium position of the balance, but on the other side.
If the apparatus is again allowed to come to rest, the fiber will turn through angle 2θ in response to the reversal of the torque.

Once the torsion constant has been determined, the forces between the masses m₁ and m₂ can be determined from the measurement of this angle.

Because the masses and their separations are known, G can be calculated.

Cavendish obtained a value for G within about 1 percent of the currently accepted value given by the following Equation.
G=6.67 x 10^-11N m²/kg²