Critical Velocity in Vertical Circular motion – minimum velocity for a vertical circle

Last updated on February 12th, 2022 at 02:14 pm

Today’s topic is Critical velocity in a vertical circular motion. Once we are done with its definition we will derive the Critical Velocity formula.

Definition: The minimum velocity of an object at the highest point of the rotation while having a vertical circular motion, is called Critical Velocity. If the velocity of the object falls below this at the highest point then the object will not be able to continue in its circular path. Please note this concept of critical velocity is applicable only for vertical circular motion.

Critical Velocity Formula [ Minimum velocity at the highest point of the vertical circle] | √(gr) formula

Critical velocity formula is expressed as V1 = √(gr)
where g is the acceleration due to gravity and r is the radius of the vertical circular path being traversed by the object.
So the minimum velocity needed at the highest point to complete a vertical circle is expressed as √(gr)

Formula for the Minimum Velocity at the Lowest Point of the vertical circle to attain the Critical velocity at the highest point | √(5gR) formula

Minimum Velocity at the Lowest Point of the vertical circle to attain the Critical velocity at the highest point is expressed with the following formula:
V2 = √(5gR)

Circular motion in horizontal plane vs Circular motion in the vertical plane

Circular motion in the vertical plane has some basic differences from the same in the horizontal plane. In the last post on Centripetal Force, we have shown that while rotating in a circle in the Horizontal plane, the gravitational force has no role (no work done) on the rotating object. But during the circular motion in the vertical plane, the role of gravitation is omnipresent. The Vertical circular motion also has a concept of critical velocity, which has no connection with horizontal circular motion.

Critical Velocity Formula – derivation | Derive √(gr) formula

Let’s take a rock of mass m tied to light and inextensible string and start to rotate it along a vertical circular path of radius R.

What can be observed from its motion? Yes, it’s not uniform.

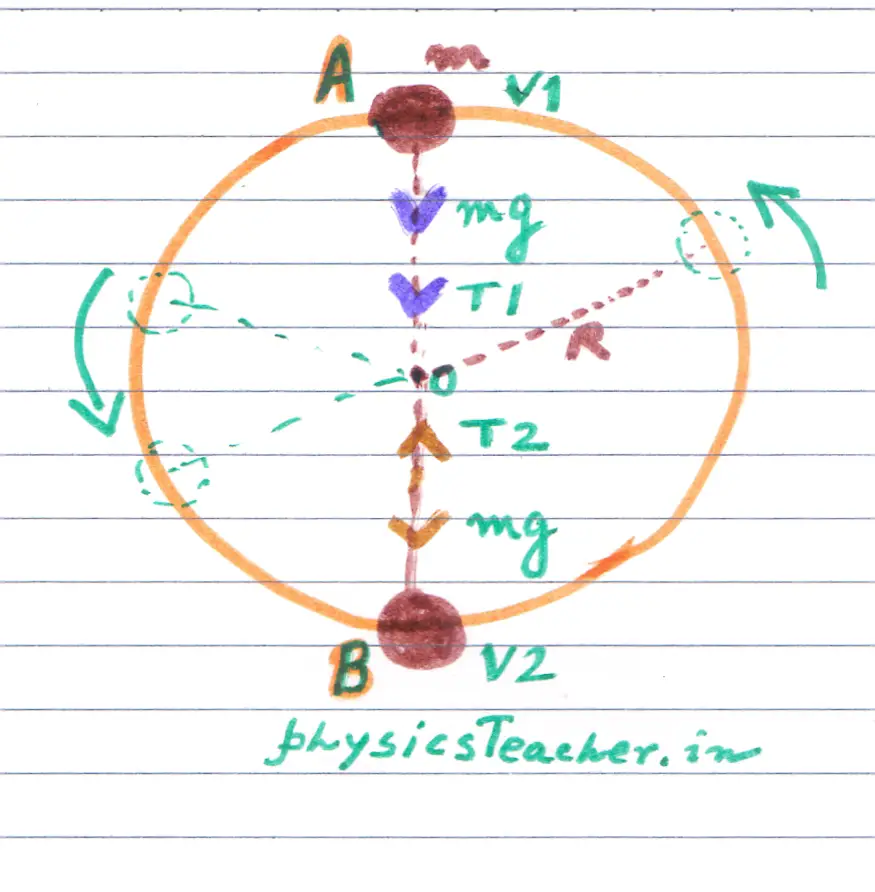
While descending from the highest point (A) of the circular track to the lowest point B, its velocity gradually increases. Also, the tension of the string increases gradually as the rock comes from A to B. If you rotate the rock with the string tied with your finger, then you can feel this difference.

Let’s consider that the velocity at A and B are V1 and V2 respectively. Here we have to consider the Tension in the string as well.

Now please note that both at A and B, the net force required for the circular motion to continue is Centripetal Force. (designated as CF in the following diagrams)

As we know, Centripetal Force is a real force that has to be provided by some agent/s or it’s to be generated by the mutual interaction of multiple agents in a system.

Now we will analyze with Free Body diagrams to find out who supplies this centripetal force at points A and B.

derivation √(gr) formula with FBD

At the highest point (A) if we consider the forces acting on the rock then these are,

(i) The weight (mg) of the rock acting vertically downwards
(ii) The tension exerted by the string (T1) on the rock (direction is away from the rock along the string)

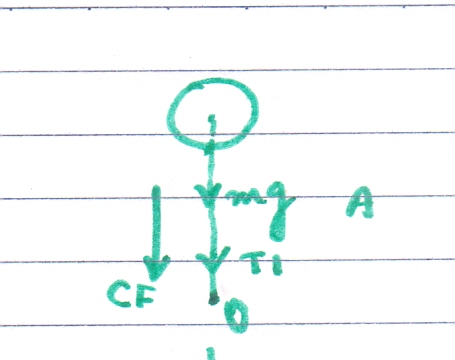
So these 2 forces are mutually acting to supply the required Centripetal force at point A.

Now considering the position of A, all these 2 vectors are pointing vertically downwards i.e. towards the center.

So we can write this equation for point A

  T1 + mg = (mV1^2)/R ……………………..(1)

Now consider point B. The force components acting on the rock here are as listed below:

(i)The weight (mg) of the rock is acting vertically downwards.
(ii) The tension exerted by the string (T2) on the rock (As said earlier, the string tension at B is more than that at point A. We mark this say, as T2)

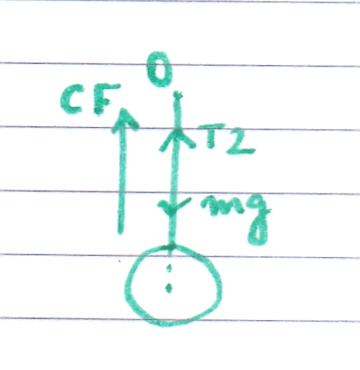
Again if we consider the position of B, the weight acts vertically downwards. The direction of T2 is again away from the rock and along the string, so at B it’s vertically upwards. As these 2 force components mutually act to supply the centripetal force at point B also, so we can write this equation for the point B

T2 – mg = (mV2^2)/R …………………….. (2)

Now let’s move towards deriving the expression of Critical Velocity.

At the highest point, let’s consider that the tension of the string is zero (T1 = 0) and the weight of the rock is sufficient enough to supply the centripetal force required to sustain the circular motion.

In that case, we can write,
mg = (mV1^2)/R

Critical Velocity formula or Equation

V1 = √(gr) …………………….. (3) 

Please note that this is the minimum velocity at point A which can keep the rock in its circular path. If its velocity falls below this value, then the string will slack and the rock will drop down finally.

Derivation of formula for the Minimum Velocity at the Lowest Point to attain the Critical velocity at the highest point | Derive √(5gr) formula

We can easily calculate the expression of the minimum value of V2 at point B (the lowest point of the circular path at a vertical plane), which is a must to maintain the Critical Velocity at point A (the highest point).

Note that the height difference between A and B is the diameter of the circle = 2R

Total Energy of the rock at point B (the lowest point) = its Kinetic energy = ½ . mV2^2 ………….. (4)

Total energy of the rock at point A (the highest point) = its Kinetic Energy + its Potential Energy

= ½ .mV1^2  +  mg. (2R)

= ½ .m.gR + 2mgR      [ substituting V1 with critical velocity i.e. (gR)^(1/2)]

=(5/2)mgR ………………..(5)

Equating equations 4 and 5 following the Law of conservation of energy, we get,

V2^2 = 5gR

or,  V2 = √(5gR)…………..(6)

This is the equation of the minimum velocity at the lowest point of a vertical circular motion path that is a must to avail critical velocity at the highest point of the same vertical circular motion path.

Here we have studied the concepts of Critical velocity as well as derived its expression. Also, we have derived the equation of the minimum velocity required at the lowest point of the circle, to attain just the critical velocity at the highest point of the circular track.

Related Study: Centripetal force