Numerical problem on car hydraulic braking – solving

In this post, we will solve a numerical problem based on the principle of a car hydraulic braking system.

To solve this numerical, we will take the help of the concepts of the lever, and the pressure principle of Pascal.

We will go through the problem statement first and then solve the numerical step-by-step.

Numerical on hydraulic braking principle – problem statement

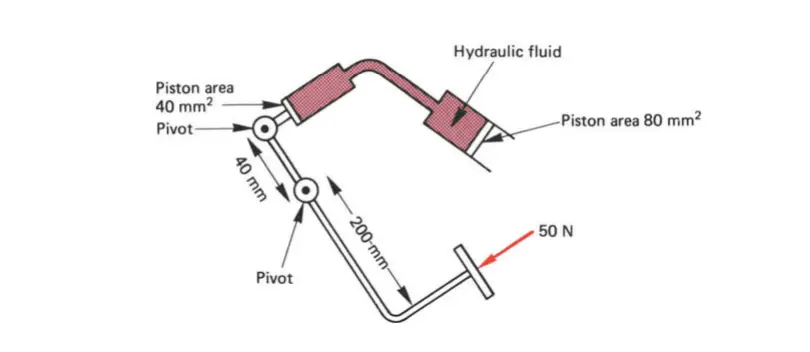
The diagram represents the principle of a car hydraulic braking system.

A force of 50 N is applied to the brake pedal, which is at one end of a lever arm. The other end of the lever arm is connected to a piston of an area of _{40 mm^2.}

A hydraulic fluid fills the space between this piston and another one of area 80 mm^2.

Using the measurements shown in the diagram and ignoring any frictional forces,

(a) State the principle of moments and use it to calculate the force on the piston of area 40 mm^2

(b) What is the pressure on the piston of an area of 40 mm^2?

(c) What is the pressure on the piston of area 80 mm^2?

(d) What is the force on the piston of area 80 mm^2?

(e) Why would it be dangerous if some air got trapped in the hydraulic fluid?

Solution:

(a) When a body is in equilibrium, anticlockwise moments = clockwise moments

50 N x 200 mm = force x 40mm

=>force = 50 N x 200 mm / 40mm

=>force on the piston of 40 mm^2= 250 N

(b) Pressure= force/area=250 N / 40 mm^2 = 6.25 N/mm^2

(c) 6.25 N/mm^2 [The pressure is transmitted throughout the fluid]

(d) Force= 6.25 N/mm^2 x 80 mm^2 = 500 N

(e) Air is compressible and if the brake pedal was pushed the force would compress the air.

The braking force applied to the second piston would be little unless the brake pedal could travel a very long way.