Centripetal Force and Washing machine – How centripetal force helps Washing machine operation

Last updated on May 1st, 2023 at 02:58 pm

Centripetal Force concepts & facts with examples and Washing machine: In this post, we will discuss the fundamental concepts of centripetal force & its real-life examples like how the centripetal force helps the Washing machine operation, etc. We’ll find out how concepts of centripetal force have been intelligently implemented in Washing machines to wash clothes.

Define centripetal force

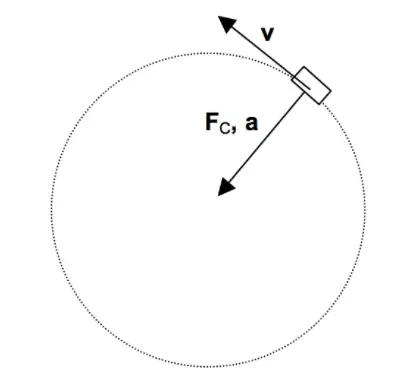
The force that provides centripetal acceleration and sustains circular motion is referred to as the centripetal force (Fc ), and its direction is always towards the center of the circle. Centripetal force is a real force that acts on an object moving in a circular path. And this force acts towards the center of the circle. This is the force that enables an object to continue its motion in a circular path. Its magnitude: F_c = mass x Centripetal Acceleration = mv²/r
where m = the mass of the object in motion, measured in kg
v = the linear orbital velocity or speed of the object in motion, measured in m/s
and, r = the radius of the circle, measured in m

Define Centripetal Acceleration

Centripetal acceleration is just the acceleration provided by the centripetal force.
Any change in velocity involves acceleration. Acceleration in circular motion is referred to as centripetal acceleration (a). It is found that this acceleration is related to the orbital speed of the (uniform) circular motion and its direction is always towards the center of the circle. The magnitude of the acceleration can be expressed as a = v²/r,
where v = the linear orbital velocity or speed of the object in motion, measured in m/s and, r = the radius of the circle, measured in meter

Centripetal force examples

We see many examples in nature where the centripetal force is being applied. Here are 5 examples of centripetal force.

• Movement of the planets around the Sun,
• movement of the moon encircling the Earth,
• The electron orbits the nucleus in an atom,
• a car or a bike taking a circular bend,
• Washing machine, etc.

Applying the concepts of this force many devices like washing machines have been designed.

Centripetal force is essential to maintain circular motion – explain

Centripetal force is essential to maintain circular motion. If it is insufficient (or has been removed) then the circular motion cannot be sustained. For instance, when a car is making a turn, it is describing an arc of a circle. What provides the centripetal force is the friction between the tyres and the road.

If the road is covered by ice, the friction between the tyres and the road is greatly reduced. Consequently, the centripetal force may not be sufficient to sustain the circular motion, and the car then skids off the road by maintaining its linear velocity.

How centripetal force helps Washing machine operation | Centripetal Force and Washing machine physics

Let’s see how centripetal force helps a washing machine to operate and wash clothes. Concepts of centripetal force are behind washing machine functionality. As clothes are put inside the drum and the drum is filled with water and the power supply is switched on, a circular motion sets into the drum.

The circular motion of the drum transmits a similar motion to the clothes as well. But as the clothes are not physically attached to the center of the drum, they don’t get any centripetal force to continue the circular motion uniformly.

As a result, they tend to move in a straight line tangent to the circular path. But they face the drum body on their way, hit it forcefully, and revert back. The rotating drum again injects circular motion into the clothes and this cycle continues.

But this doesn’t happen to the water droplets in the clothes. As the clothes hit the drum body, as described above, the water droplets make their way to the outside of the drum, through the holes on the drum body. And the clothes get rid of the water(and dirt) by the time the washing cycle completes. This briefly describes washing machine physics.

Is there any contribution of centrifugal force in the washing machine operation?

No. As said above centrifugal force is a pseudo force. It does not have any contribution to the Washing machine. The centripetal force concept is behind the washing machine operation.

washing machine works on which force?

Application of Centripetal force is observed in washing machines.

centrifugal force washing machine | washing machine centrifugal force – any connection?

Centrifugal force is a pseudo force. It does not have any contribution to the Washing machine operation.

washing machine is centripetal or centrifugal?

The washing machine is built upon the functionality & feature of centripetal force.

---

Is centrifugal force a reaction of centripetal force?

No. Centrifugal Force is not a reaction force of the centripetal force. Centrifugal Force is a pseudo-force that doesn’t even exist in reality. So it can’t be a reaction force. The reaction force for centripetal force is actually known as Centrifugal Reaction.

How Is Centrifugal Reaction the reaction force of centripetal force? Explain this with Newton’s 3rd Law

As per Newton’s 3^rd Law, Centripetal Force must be having an equal and opposite reaction force.

Yes, it has. It’s called Centrifugal Reaction. Please note that it’s not the same as Centrifugal Force. The concept of centrifugal force is completely different and it’s not even a real force.

Coming back to Centrifugal Reaction! When we rotate a piece of stone with our finger through a tied string, then the finger also feels a force that is applied by the rotating stone. This is a Centrifugal Reaction force.

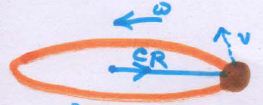
Now as its direction is opposite to the Centripetal force (finger feels a force which tries to drag it outwards, away from its central position), it’s Centrifugal, and as it’s a reaction force, so we call it Centrifugal Reaction force. (CR in the Diagram above).

Pls, note that: Centrifugal reaction is not centrifugal force.

Difference between centripetal force and centrifugal force

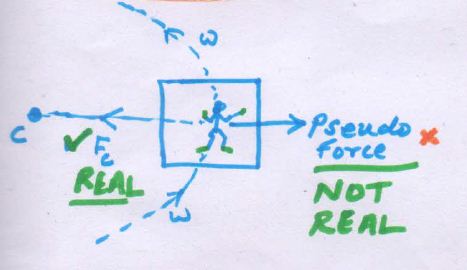
Centrifugal Force is a pseudo force, it’s not a real force. But, Centripetal force is a real Force because it evolves due to the mutual interaction of objects or masses. Centrifugal force is felt only within a Rotating Frame of Reference but doesn’t exist in reality.

If a person shares the same frame of reference as a rotating object, then that object will apparently look like a static object to that person.
The person within a rotating frame of reference will never understand the reason for Centripetal Force being applied because for him that frame of reference is static and for something static, there is no need for any force to be applied.

Rather he will feel as if some external force is being applied which is pulling the entire system away from the central position and there is another force directed towards the center which is balancing the first one.

What is the Centripetal Force formula?

The formula of Centripetal force is F= mass x Centripetal Acceleration = mv²/R = mω²R, where m is the mass of the object moving in a circular path, ω is the angular velocity of that object, and R is the radius of the circular path.

Now, let’s list down the features of circular motion evident from the Centripetal force formula.

What we come to know from the Formula of centripetal force | Characteristics or features of Centripetal force | Facts on centripetal force

The features of circular motion evident from the Centripetal force formula are listed below:

1) An object with more mass would be requiring less angular velocity and a smaller radius of circular motion, to maintain its circular motion.

2) If R is high, even a lower angular speed can keep an object rotating in a circular path.

3) If R is too small, then angular velocity has to be at the higher side to compensate for the small R and generate the necessary Centripetal Force required to continue the circular motion.

Also see: Numerical problems based on Centripetal force concepts

why is the centrifugal force called a pseudo force?

Centrifugal force is called a pseudo force or non-existing force. Let’s find out why. When passengers travel in a bus and the bus takes a sharp turn, then the passengers feel thrust in the opposite direction. Here the bus is an example of a Rotating Frame of Reference and the passengers within that frame of reference feel a pseudo force, an unreal force! (see the diagram below) This pseudo force is called Centrifugal Force.

The road beside the bus is a static frame of reference.

A person standing in that static frame will never reciprocate the presence of centrifugal force for that bus, to him the movement of the passengers is just because of directional inertia.

how is this centripetal force being applied to the stone being rotated by a string?

When a stone is rotated by a string tied with a finger then the centripetal force is transferred from the finger to the stone and this transfer is happening via the string only.

Who is supplying this centripetal force here? The finger.

That’s why when the string is released or the string is torn this force can’t pass to the stone anymore. This is the instance when Newton’s First Law of Motion comes into play. As there is no force (net force) on the stone so it will continue along its last direction on the circular path. And the direction is actually the tangent to that point on the circular path.

Centripetal Force is a real force – Who or What is supplying this?

Any force can be a centripetal force. Centripetal force is the umbrella term given to any force that is acting perpendicular to the motion of an object and thus causing it to go in a circle.

1) In the above example, a stone is rotated in a horizontal plane with a string tied with a finger. Here the finger supplies the required centripetal force that makes the stone rotate. There are a few other instances when the supplier of this force varies from case to case.

2) Electron orbits the nucleus in an atom. The electrical attraction force generated between an electron and the nucleus supplies the centripetal force on the electron.

3) A car or a bike taking a circular bend – The Frictional force between the tires and the road supplies the required Centripetal force. (As it is a frictional force so certainly it has a maximum limit, beyond which balancing in a bike at a circular bend won’t be possible. It’s a different story, will take this in a separate post)

4) The satellite revolves around the earth. Here Gravitational Attraction between the earth and the satellite supplies this centripetal force.

List of Common circular motions and the suppliers of centripetal force (in tabular format)

Any force can be a centripetal force. Centripetal force is the umbrella term given to any force that is acting perpendicular to the motion of an object and thus causing it to go in a circle.

Motion	Provider of centripetal force
Whirling rock on a string	The string
Electron orbiting atomic nucleus	Electron nucleus electrical attraction
Car cornering	Friction between tyres and road
Moon revolving around Earth	Moon–Earth gravitational attraction
Satellite revolving around Earth	Satellites revolving around Earth

Is centripetal force real?

Note that this centripetal force is a real force. In all the above examples, you can see that this force is supplied by real forces like gravitational force, electric force, or frictional force.

Centrifugal force, on the other hand, is a pseudo-force.

When can Gravity Act as a Centripetal Force?

The force of Gravity causes an attraction between two objects of mass m1 and m2 at a distance of r and this force is expressed as F_g = Gm₁m₂/r²

By Newton’s Third Law, both objects experience the force: equal in magnitude and opposite in direction, and both will move as an effect of it.

If one of the objects is much lighter than the other (like the earth is to the sun, or a satellite is to the earth) we can approximate the situation by saying that the heavier mass (the sun) does not move, since its acceleration will be far smaller due to its large mass. (acceleration= force/mass)

Then, if the lighter mass remains at a relatively constant absolute distance from the heavier one (remember, the centripetal force needs to be constant in magnitude), we can say that the lighter mass experiences an effective centripetal force.

Gravity is not always a centripetal force. This is a really important point. It only acts as a centripetal force when conditions approximate those listed above.

The math of Centripetal Gravity | Equation of Centripetal gravity

If gravity provides centripetal force and acceleration, we can write the following equation.
F_g = Gm₁m₂/r² = m₁ v² /r …………… (i)
It’s important to remember that m1 refers to the lighter mass since that is the one traveling. Then simplifying (i),
Gm₂=v². r ………………………… (ii)
r is the radius of the orbit and v is the orbital velocity.

Friction Acting as a Centripetal Force – a case study

Question: Mr. Carracer buys new tires for his car in order to take turns a little faster. The new tires double the coefficient of friction with the road. With the old tires, he could take a particular turn at a speed of v_i. What is the maximum speed he can now take the turn without skidding out?

Solution: To find the maximum speed a car can take a corner on a flat road without skidding out, set the force of friction equal to the centripetal force.
This is because the centripetal force pushes the car off the road and the frictional force keeps the car on the road. Therefore, if the centripetal force(F_c) and the frictional force(F_k) were equal, the car would be going the maximum speed it could go on that turn without sliding off the road.
F_c = mv_i² /r =F_k
So initial speed = v_i = (r F_k m)^1/2 ………………..(a)

Now when the coefficient of friction is doubled, the frictional force is also doubled. Hence with the new tires, the frictional force becomes 2F_k.
And the final speed = v_f = (r 2F_k m)^1/2 ………..(b)

So taking the ratio of v_f and v_i we get that the final speed is 2^1/2 =1.414 times of the initial speed.
Here it’s pretty evident that higher friction supplies the higher value of centripetal force and that in turn, enables the car to get more speed while taking the bend without skidding out.

Take Away | Related Topics For You

In this post, we have studied a specific application of centripetal force to run a washing machine.

I hope you enjoyed this post. We will discuss more in this line! Now watch an informative VIDEO below!

 More Study Suggestions:

1) Critical Velocity in Circular motion in the vertical plane

2) Circular Motion and its relationships with linear motion