Angular Motion & Linear Motion Quantities – derivation of 3 relations

Last updated on May 24th, 2023 at 12:08 pm

In this post, we will focus on the definitions of circular motion and linear motion first which will show their basic differences as well. In addition to this, we’ll derive a couple of important relationships between the quantities of circular motion and linear motion.

We will derive the following:
a) Relationship between angular displacement and linear displacement
b) Relationship between angular velocity and linear velocity
c) Relationship between angular acceleration and linear acceleration

What is Circular Motion?

The circular motion of an object is its movement along the circumference of a circle. You can define it as the rotation of an object along a circular path.

It can be uniform, with a constant angular rate of rotation, or non-uniform with a changing rate of rotation.

What is Linear Motion?

Linear motion or Rectilinear motion is a one-dimensional straight-line motion. This type of motion describes the one-dimensional movement of a particle or a body.

A body experiences rectilinear motion if any two particles of the body travel the same distance along two parallel straight lines.

Examples of Linear Motion Quantities

Let’s list down the variables of Linear motion first.

The most basic quantities of linear motion are Distance traveled, Displacement, time, etc. The next level quantities of linear motion are Speed, Velocity, Acceleration, Momentum, etc. We discussed already (in a previous post) the difference between distance traveled and displacement and the difference between speed and velocity.

Examples of Circular Motion Quantities

The variables mentioned in the Linear motion section have their individual counterparts in the case of Circular Motion. Examples of circular motion quantities include angular displacement, angular velocity, and angular acceleration.

We will discuss some of these in this post and draw a relation with their Linear Motion counterparts.

Angular Displacement and Linear Displacement Relationship [derivation]

We will derive the Relationship between angular displacement and linear displacement. Say a point object is moving in a circular path of radius r. Let’s say the center of this circular path is O.

At some point in time say the particle is at point P on the circumference of the circle. At this moment the radial vector of this motion is OP.

After a time gap of t, the position of the object becomes Q (obviously on the circumference of the same circle) and the radial vector is OQ.

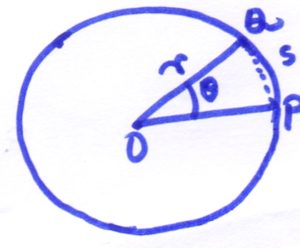
Now say the angle between OP and OQ is θ (theta). Hence the angular displacement of the particle in time duration t is θ.

In addition to this angular displacement, the particle is having a linear displacement as well when traveling from point P to Q.

Here PQ is the linear displacement, and say it is designated as s.

Now consider the right-angled triangle ΔOPQ.
Here using the Trigonometry we get, Sine θ = PQ /OQ = s/r ________________ (1)  [ Note: OQ is the radius r of the circle ]

Now, as per Trigonometry, if the angle θ is very small then Sine θ is equal to θ.

So from equation (1), we get

 θ = s/r  i.e., s= θ r ______________(2).

Here we get the relation between linear displacement and angular displacement.

Linear Displacement = Angular Displacement x Radius of the Circular path

Angular Velocity and Linear Velocity relationship [derivation]

In this section, we will derive the Relationship between angular velocity and linear velocity. During the circular motion, an object experiences angular displacement as well as linear displacement, therefore it will have angular velocity as well as linear velocity at any position on the circle.

The direction of the linear velocity of the rotating object at any point is along the tangent to the circle drawn at the point where the object is positioned at that moment on the circumference of the circle.

And angular velocity is being made by changing the angular position with time. Angular velocity is identified with the sign omega (ω). And ω = θ /t  _________(3).

At the same time, we can calculate the linear velocity as the following: linear velocity(v) = linear displacement per unit time = s/t,

v = s /t = (θ r)/t= (θ /t). r=ω.r   

or, v=ω.r ___________________(4)

Linear Velocity = Angular Velocity x radius

Angular Acceleration and Linear Acceleration relationship [derivation]

Here we are going to derive the relationship between angular acceleration and linear acceleration. Say at point P the linear velocity of the object in the rotation is V1. In addition to this at point P, the angular velocity of the rotating object is ω1.

Similarly, at point Q these are V2 and ω2 respectively.

So from equation 4, you can say that V1= ω1.r and V2 = ω2.r

We already said that the time taken to travel from P to Q is t.

Therefore we get the equation of linear acceleration (f)= (V2-V1)/t = (ω2. r – ω1.r)/t= (ω2-ω1)r/t = α r

where Alpha (α) = (ω2-ω1)/t = Rate of change of Angular Velocity = Angular Acceleration.

So we see f = α r

Linear Acceleration = Angular Acceleration x Radius

Read this post for a quick summary listing the relationships between linear and angular variables.

Numerical problems – circular motion

Assuming you know these:
 RPM means Revolutions per minute,
 RPS means revolutions per second and 180 degree = π radian
and  π=22/7

Q1 ) An electric fan was rotating with a speed of  210 rpm. Its velocity is increased to 630 rpm in 11 seconds with the help of a regulator.
Calculate the angular acceleration of the fan.

Solution:

The initial angular velocity = ω1 = 210 rpm = 210/60 rps = (2 π .210)/60 radian/second  = 7 π rad/s
And the final angular velocity =  ω2 = 630 rpm = 630/60 rps = (2 π .630)/60 radian/second = 21 π rad/s

Time elapsed =t= 11 seconds.

So Angular acceleration of the fan (α) 

= change in angular velocity/time elapsed

i.e. (ω2 –ω1)/t =(21π – 7π ) /11 rad/s^2 = 14π /11 rad/s^2
= (14/11) X(22/7) rad/s^2 = 4 rad/s^2   (answer)

Summary

In this post, we have defined both circular motion and linear motion with examples of physical quantities related to these 2 types of motion. Here in this post, we have derived the following as well:

a) Relationship between angular displacement and linear displacement

b) Relationship between angular velocity and linear velocity

c) Relationship between angular acceleration and linear acceleration

We have solved one numerical problem related to circular motion as well.

Now you can share this post as much as possible! Use the social media buttons on this page!