Apparent weight in an elevator – analysis of the bathroom scale reading

We will talk here about a person’s Apparent weight in an elevator referring to bathroom scale reading in the elevator.

The apparent weight of a person in an elevator depends on the direction and magnitude of the elevator’s acceleration.

• When the elevator is at rest or moving at a constant speed (i.e., acceleration is zero), the apparent weight is equal to the person’s actual weight. 
  Bathroom scale reading in the elevator = person’s actual weight
• If the elevator is accelerating downwards, the apparent weight is less than the actual weight. This causes a feeling of lightness.
  Bathroom scale reading in the elevator = less than the person’s actual weight
• If the elevator is accelerating upwards, the apparent weight is more than the actual weight. This causes a feeling of heaviness.
  Bathroom scale reading in the elevator =more than the person’s actual weight
• If the elevator cable breaks, both the person and the elevator will accelerate downward with the gravitational acceleration g. Since the person’s weight is all that is required to give him that acceleration, the normal force acting on his feet must then be zero.
  The Bathroom scale reading will likewise be zero, and the person is apparently weightless!

Analysis

Probably all of you have had the experience of riding an elevator and feeling sensations of heaviness or lightness as the elevator accelerates up or down.

A few questions arise here in our mind:

Do we really weigh more or less than usual in these situations?
If we take a bathroom scale into the elevator, will it read our true weight when the elevator is accelerating?
How can we apply Newton’s laws of motion to explore these questions?

The first step in analyzing any situation using Newton’s laws is to isolate the body of interest and carefully
identify the forces that act on just that body.

• In this case, we will isolate the person standing on the scale, since her weight is the focus of our questions.
• The second drawing shows a free-body diagram of the woman indicating just those forces that act on her.
• In this case, just two other objects interact with the woman, resulting in two forces.
• The Earth pulls downward on the woman through the force of gravity W. The scale pushes upward on her feet with a force N, the normal force.
• The vector sum of these two forces determines her acceleration.

Apparent weight in an elevator If the elevator is accelerating upward

• If the elevator is accelerating upward with acceleration a, the person must also be accelerating upward at that rate.
• The net force must also be upward, which implies that the normal force N is larger than the gravitational force W.

Using signs to indicate direction, and letting the positive direction be upward,
Newton’s second law requires that
Fnet = N – W = ma.
=> N – mg = ma
=> N = m(g+a) ……………. (1)
which implies that in this case (the elevator is accelerating upward) the normal force N is larger than the gravitational force W. This causes a feeling of heaviness.

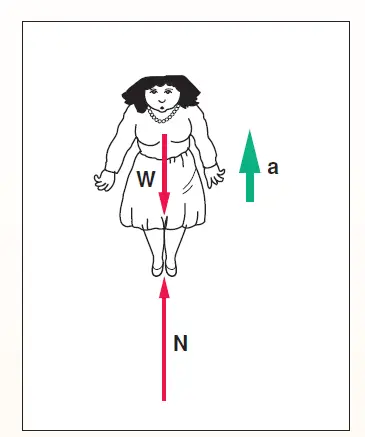
Scale Reading when the elevator is accelerating upward

What about the scale reading? By Newton’s third law, the person exerts a downward force on the scale equal in size to the normal force N, but opposite in direction. Since this is the force pushing down on the scale, the scale should read the value N, the magnitude of the normal force. The person’s true
weight has not changed, but his apparent weight as measured by the scale has increased by an amount equal to m a.
As per equation (1) we got above, in this case the scale reading: N = m(g+a)

Apparent weight in an elevator If the elevator is accelerating downward

• If the elevator is accelerating downward with acceleration a, the person must also be accelerating downward at that rate.
• The net force must also be downward, which implies that the normal force N is less than the gravitational force W.

Using signs to indicate direction, and letting the positive direction be downward,
Newton’s second law requires that
Fnet = W – N = ma.
=> mg – N = ma
=> N = m(g-a) ……………. (2)
which implies that in this case (the elevator is accelerating downward) the normal force N is less than the gravitational force W. This causes a feeling of lightness.

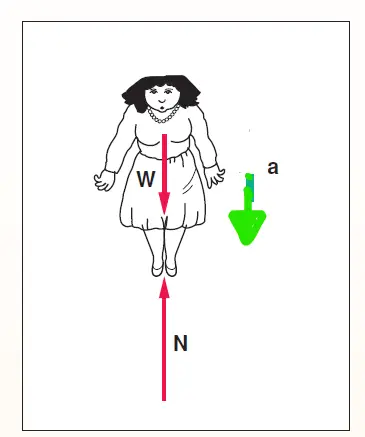
Scale reading when the elevator is accelerating downward:

In this case, the scale reading N will then be less than the woman’s true weight by the amount ma

Apparent weight in an elevator If the elevator is at rest or moving at a constant speed

When the elevator is at rest or moving at a constant speed (i.e., acceleration a is zero), the apparent weight is equal to the person’s actual weight. 
N = W
=>N=mg ……….. (3)

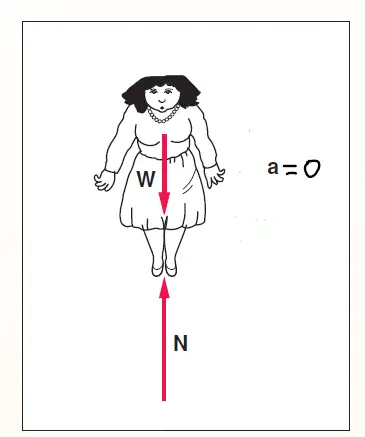
If the elevator is at rest or moving at a constant speed then:
Bathroom scale reading in the elevator = person’s actual weight

If the elevator cable breaks

If the elevator cable breaks, both the person and the elevator will accelerate downward with the gravitational acceleration g.

W – N = mg [here downward acceleration = a = g]
=>mg – N = mg
=>N = 0 ……. (4)

Since the person’s weight is all that is required to give him that acceleration, the normal force acting on his feet must then be zero.

The Bathroom scale reading will likewise be zero, and the person is apparently weightless!