Rotational kinetic energy derivation class 11

Last updated on July 12th, 2023 at 03:54 pm

In this post on Rotational kinetic energy derivation class 11, we will derive the Rotational Kinetic Energy Equation in a few easy steps. This equation expresses the kinetic energy of a rotating object just because of its rotational motion. So, let’s begin the derivation.

Rotational kinetic energy derivation class 11 | Derive Rotational kinetic energy equation or expression

To derive the rotational kinetic energy equation, here we will consider the rotating blades of a wind turbine. We can easily see that the blades of a wind turbine have no overall translational motion. Still, each particle in the blades is moving and hence has kinetic energy.

Now if we add up the kinetic energy of all the particles that make up the blades, we will find the rotational kinetic energy of the blades. Remember that this kinetic energy is just due to rotation.

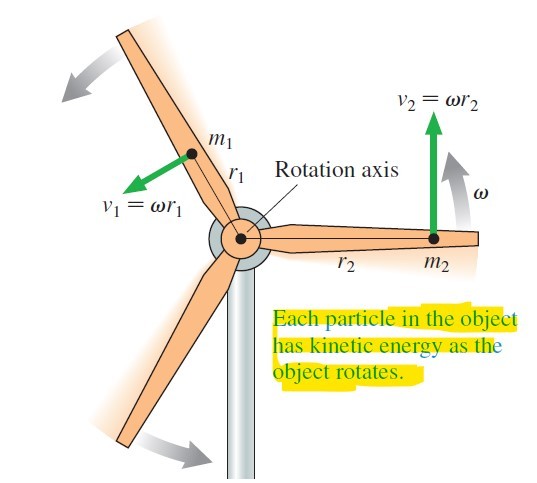
In Figure 1, we will consider the motion of two particles in the wind turbine blades. Say, the blade assembly rotates with angular velocity ω. Recalling from our post on linear motion and circular motion a particle moving with angular velocity ω in a circle of radius r has a speed v = ω r.

Please note that depending on the position of the particle on the blades they will have different speeds and radii. But all of these particles will have the same angular velocity.

Thus particle 1, which rotates in a circle of radius r₁, moves with speed v₁ = ω r₁ and so has kinetic energy = (½) m₁v₁² = (½) m₁ (ω r₁)² = (½) m₁ ω² r₁².

Similarly, particle 2, which rotates in a circle with a larger radius r₂, has kinetic energy = (½) m₂ ω² r₂².

The object’s rotational kinetic energy is the sum of the kinetic energies of all the particles: K_rot = (½) m₁ ω² r₁² + (½) m₂ ω² r₂² + ….. = (½) (Σmr²) ω² ……….. (1)

Now, Σmr² is known as the moment of inertia I, which is the rotational equivalent of mass or inertia.

Thus the Rotational Kinetic Energy = (½) I ω² ……………… (2)

The above equation is the equation for the Rotational kinetic energy of an object with a moment of inertia I and angular velocity ω.

Now you may solve some numerical problems here: Numerical problems based on the Rotational Kinetic Energy formula

Summary | Take Away | Suggested Study

In this post, we have adopted a step-by-step approach to derive the equation of the rotational KE. We have seen how angular velocity and moment of inertia have become parts of that KE formula.

Now it’s your turn to share this using the share buttons on the page.

Here, we would suggest a few related posts for your reading that might help for easier understanding. The suggested posts are:

Moment of Inertia of different bodies

Relationship between linear motion and circular motion quantities

Numerical problems based on the Rotational Kinetic Energy formula