Pure Rotational Motion of rigid bodies
In this post, we will discuss the Pure Rotational Motion of rigid bodies, and also analyze an example with a supporting diagram. Then we will discuss Pure translational motion with a diagram. Once we do these, we will quickly compare Pure Rotational Motion and Pure translational motion.
Pure Rotational Motion of rigid bodies – characteristics & equations
In pure rotation of the rigid body, the axis of rotation is fixed and the system does not have any translational motion. The angular velocity and angular acceleration of all particles of the system are the same. However, the velocity and acceleration of different particles of the systems are different (because their distances from the axis of rotation are different).
For example, rotation of a ceiling fan, rotation of the blades of a windmill, rotation of fixed pulleys, rotation of hinged doors and windows, a bicycle on its stand with the rear wheel rotating, etc., can be analyzed as pure rotation.
The problems involving pure rotation can be analyzed using the kinematic equations for rotational motion and applying the equation τ = I α, where τ is the net torque about the axis of rotation, I= moment of inertia of the rigid body about the axis of rotation, and α = angular acceleration of the rigid body about the axis of rotation.
Conventionally anticlockwise torque is taken as positive and clockwise torque as negative.
Figure 1 below shows a uniform disc of mass M and radius R, in pure rotation about a fixed axis through its center, with a constant angular velocity ω.
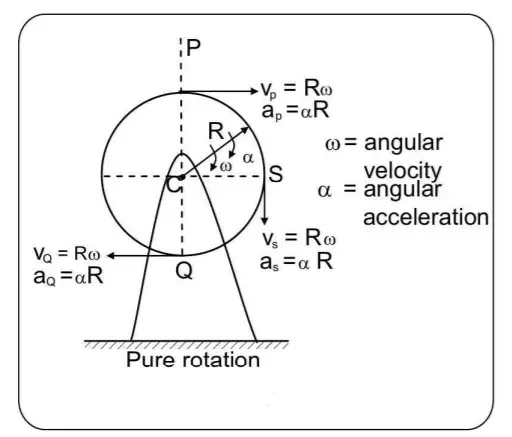
The velocity of points P, S, and Q on its rim have the same magnitude = Rω but their directions are different. The center C of the disc is at rest.
Pure translational motion
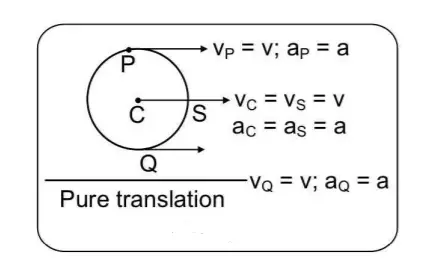
If the brakes of a bicycle are applied and the bicycle is moved forward, the wheels of the bicycle will be in pure translation. This situation is shown below in figure 2.
If the center C is moving with a velocity v and acceleration a then all points P, Q, and S also have the same magnitude and direction of velocity as well as acceleration as that of point C.
difference between Pure Rotational Motion & Pure translational motion
Pure Rotational Motion: In Pure Rotational Motion, the velocity of different points on the rim (points P, S, and Q in figure 1) of the disc have the same magnitude = Rω but their directions are different. The center C of the disc is at rest. So in the case of Pure Rotational Motion, the center of the disc remains at rest.
Pure translational motion: If the center is moving with a velocity v and acceleration a then all points on the rim of the disc (points P, S, and Q in figure 2) also have the same magnitude and direction of velocity as well as acceleration as that of the center of the disc.
