Small Angle Approximations (for physics derivations and numerical problems)

For very small angles, you can approximate values for the sine, cosine, or tangent. This is useful when calculating the fringe separations in interference patterns.

When θ is measured in radians, a small angle segment approximates to s/r where s is the arc length and r is the radius. In other words, for a small angle segment, we can write, θ = s/r.

The rules for Small Angle Approximations are:

sin θ ≈ tan θ ≈ θ
cos θ ≈ 1

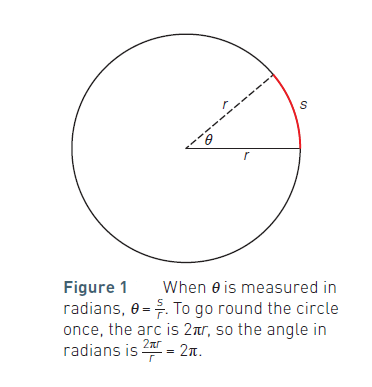
To convert the angle in radians into an angle in degrees, remember that one radian is 180/π ≈ 57.3 degrees.

Exercise:

Use the small-angle rule to write down these values:
a) tan 0.01 radians
b) cos 0.05 radians
c) sin 0.03 radians.