Rotational Kinematics Numerical Problems and solutions
Last updated on April 12th, 2021 at 09:27 am
This post is all about Rotational Kinematics Numerical Problems and solutions. We will use the following four rotational kinematic equations (presented together with their translational counterparts) to solve the numerical problems.
Rotational kinematic equations | equations used to solve rotational motion numerical
In these equations, the subscript 0 denotes initial values (ω0 and vo are initial values). The 4 equations in the first column represent the rotational kinematics. The second column consists of the translational equivalents.
| Rotational Kinetic equations | Translational kinetic equations | Constants |
|---|---|---|
| θ=(1/2)(ω0 + ω)t | s=(1/2)(vo + v)t | α, a |
| ω = ω0 + αt | v = vo + at | α, a |
| θ=ω0t+(1/2)αt2 | s=v0t+(1/2)at2 | α, a |
| ω2 = ω02+ 2αθ | v2 = vo2 + 2as | α, a |
Numerical problem on Angular Displacement | Rotational Kinematics Numerical
1. A rigid body turns through 1.85 radians. Express this in degrees and revolutions.
Solution:
Using the fact that π radians equal 180 deg, then
1.85 rad = (1.85 rad)(180 deg /π rad) = 106 deg ……….(1)
Then, using the fact that 1 revolution = 2π rad to get
1.85 rad = (1.85 rad)(1 rev / 2π rad) = 0.294 rev ……………… (2)
Rotational Kinematics Numerical on Angular Velocity and Acceleration
2. Long ago people listened to music which was stored on “phonograph records”. These records turned at a rate of 33.3 revolutions per minute. Express this rotation rate in radians per second.
Solution:
Using the relations 1 rev = 2π rad as well as 1 min = 60 s to convert the units:
33.3 rpm = 33.3 rev/min = (33.3 x 2π ) rad / 60 secs = 3.49 rad/s
Numerical problem on Rotational Motion with Constant Angular Acceleration
3. A flywheel has a constant angular deceleration of 2.0 rad/s2. (a) Find the angle through which the flywheel turns as it comes to rest from an angular speed of 220 rad/s. (b) Find the time required for the flywheel to come to rest.
Solution(a)
α = – 2.0 rad/s2
ω0 = 220 rad/s
ω = 0
θ = ?
Using this rotational kinematics equation: ω2 = ω02+ 2αθ
=> 0 = 2202+ 2.(-2).θ
=> θ = (220 x 220) / 4 = 12100 rad = 1.21 x 104 rad
Solution (b)
α = – 2.0 rad/s2
ω0 = 220 rad/s
ω = 0
t = ?
ω= ω0+ αt
0 = 220 + (-2)t
t = 110 sec
Rotational Kinematics Numerical based on the Relation Between Angular and Linear Quantities
4. A string trimmer is a tool for cutting grass and weeds. It utilizes a length of nylon “string” that rotates about an axis perpendicular to one end of the string. The string rotates at an angular speed of 47 rev/s, and its tip has a tangential speed
of 54 m/s. What is the length of the rotating string?
Solution:
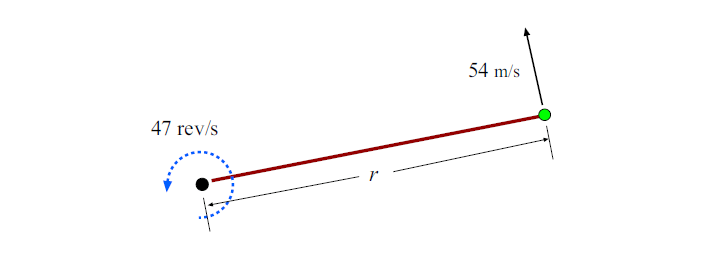
The rotating string is shown in Fig. 1. The angular velocity of the string’s rotation is
ω= 2πf = 2π(47) rad/s = 295 rad/s
We have the speed of the tip of the string (which is a distance r from the axis), and this is the linear speed v.
v= 54 m/s
Now from Equation v=ωr, we can get the length of the string, r:
r =v/ω = 54/295 m = 0.183 m
So the string is 0.183 m long.
Suggested Post
Deriving the Relations Between Angular and Linear Quantities – an easy guide
