Derivation of the total Kinetic energy Equation for Combined Translation and Rotation | Rotation of a rigid body about a moving axis

Last updated on April 12th, 2021 at 04:07 am

Before going for the Derivation of the equation of total Kinetic energy of a body under combined translation and rotation, let’s do some analysis of the dynamics of Rigid-Body Rotation About a Moving Axis to some cases in which the axis of rotation moves.

When that happens, the motion of the body is a combination of translation and rotation.

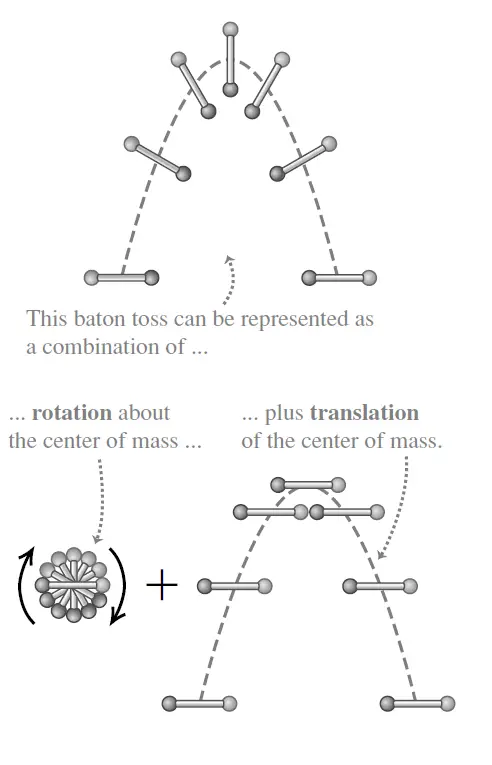
The key to understanding such situations is this: Every possible motion of a rigid body can be represented as a combination of translational motion of the center of mass and rotation about an axis through the center of mass.

This is true even when the center of mass accelerates so that it is not at rest in any inertial frame.

Example of combined translation and rotation | with diagram

Figure 1 illustrates this for the motion of a tossed baton: The center of mass of the baton follows a parabolic curve, as though the baton were a particle located at the center of mass. Other examples of combined translational and rotational motions include a ball rolling down a hill and a yo-yo unwinding at the end of a string.

Kinetic energy Equation for Combined Translation and Rotation: Energy Relationships

We will discuss here the kinetic energy of a rigid body that has both translational and rotational motions.

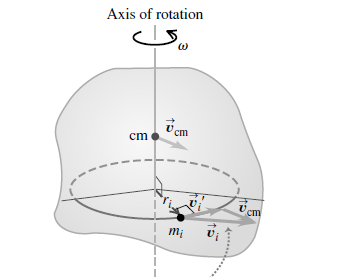
In this case, the body’s kinetic energy is the sum of a part (1/2)Mv_cm² associated with the motion of the center of mass and a part (1/2)I_cmω² associated with rotation about an axis through the center of mass.

Kinetic energy Equation for Combined Translation and Rotation = KE = (1/2)Mv_cm² + (1/2)I_cmω² (for a rigid body with both translation and rotation)

Derivation of the total kinetic energy equation for combined translation and rotation of a rigid body about a moving axis

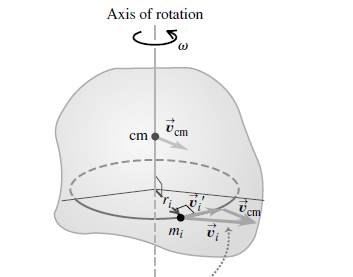
Derive the formula for total Kinetic energy for Combined Translation and Rotation: To prove this relationship, we again imagine the rigid body to be made up of particles. Consider a typical particle with mass m_i as shown in Fig. 3. The velocity v_i of this particle relative to an inertial frame is the vector sum of the velocity v_cm of the center of mass and the velocity v_i^’ of the particle relative to the center of mass:

around the center of mass. Using the formula v = ωr, we can write the last term as (1/2)I_cmω² ,
where I_cm is the moment of inertia with respect to the axis through the center of mass and ω is the angular speed.

So the equation becomes: KE = (1/2)Mv_cm² + (1/2)I_cmω² (for a rigid body with both translation and rotation)

Related Study for reference:

Here we have derived the formula of Kinetic energy of a rigid body with both translational and rotational motion. (KE for a rigid body having a combination of translation and rotation).

But there are motions that are purely rotational motions, like the rotation of a ceiling fan, rotation of the blades of a windmill, etc.

Now if you want to read about it and the KE equation for that, you must try this link to derive the equation of Kinetic energy for pure rotational motion.