Projectile Motion Formula, Equations, Derivation for class 11
Last updated on May 22nd, 2023 at 02:35 pm
In this post, we will list down the projectile motion formula set & equations, do the derivation of the Projectile Motion Equations or formulas, and find out how the motion path or trajectory looks like a parabola under the influence of both horizontal and vertical components of the projectile velocity.
We will also find out how to find out the formulas of maximum height, time to reach the maximum height, the total time of flight, range or horizontal range, & maximum horizontal range traversed by a projectile.
Quick Links:
Formulas & equations in a List
Derivations of projectile motion
- Projectile definition
- Projectile motion definition
- Projectile Motion Derivation | Derivation of Projectile Motion Equations class 11
- Derivation of the trajectory equation | Derive projectile trajectory or path formula class 11
- Equation of the Trajectory of a projectile is a parabola
- Time to reach the Maximum Height by a projectile (with derivation for class 11)
- Total time of flight for a projectile & Formula
- Maximum Height reached by a projectile & Formula
- Horizontal range of a projectile & Formula
- Greatest Horizontal Range | Maximum horizontal range (Formula derivation)
- List of Projectile motion formulas or equations derived (In Tabular format)
- Projectile motion is a superimposed motion – an observation by Galileo
- Formation of the parabolic trajectory of a projectile
- How to Calculate the velocity of the projectile at different points of its parabola trajectory?
- Give some real-life examples of projectile motion
- Force applied on a projectile and its acceleration
- Two simple rules governing the projectile motion
When an object is in flight after being projected or thrown then that object is called a projectile and this motion under the influence of constant velocity along the horizontal and downward gravitational pull along the vertical is called Projectile Motion.
Projectile definition
When an object is in flight after being projected or thrown then that object is called a projectile and this motion is called Projectile Motion. For example, the motions of a cricket ball, or baseball.
Projectile motion definition
The motion of a projected object in flight is known as projectile motion which is a result of 2 separate simultaneously occurring components of motion.
One component is along a horizontal direction without any acceleration (as no force acting in this direction) and the other is along the vertical direction with constant acceleration due to the force of gravity (considering air resistance as negligible). In the next sections, we will discuss and derive a couple of projectile motion equations.
Projectile Motion Derivation | Derivation of Projectile Motion Equations class 11
We will cover here Projectile Motion Derivation to derive a couple of equations or formulas like:
1> derivation of the projectile path equation (or trajectory equation derivation for a projectile)
2> Derivation of the formula for time to reach the maximum height
3> Total time of flight – formula derivation
4> Maximum height of a projectile – formula derivation and
5> Derivation of the formula for the horizontal range of a projectile
Students of Class 11 from boards like ISC, CBSE, and state boards will find this one useful.
Derivation of the trajectory equation | Derive projectile trajectory or path formula class 11
The trajectory of a projectile is the path that it follows during its flight. In the absence of air resistance, the path of the flight of a projectile will trace out the shape of a parabola as shown by the photograph in one of the figures below, taken with the aid of a stroboscope.
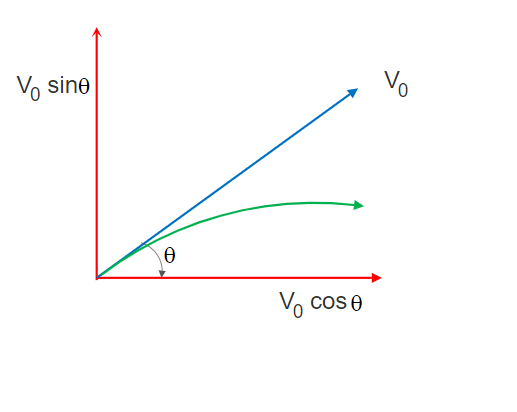
Let’s start with the derivation of the Projectile Motion Path Equation (or Projectile trajectory equation). Say an object is thrown with uniform velocity V0 making an angle theta with the horizontal (X) axis.
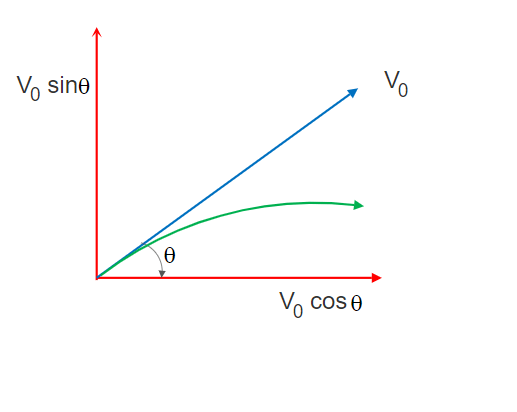
The initial velocity component along X-axis = V0x = V0 cosθ and the initial velocity component along Y-axis = V0y = V0sinθ.
(Air resistance is taken as negligible)At time T = 0, there is no displacement along the X and Y axes.
At time T=t, (i.e., for any time instant t)
Displacement along X-axis = x= V0x.t = (V0 cosθ). t ………… (1) and
Displacement along Y-axis = y = (V0sinθ ).t – (1/2) g t2 …………(2)From equation 1 we get: t = x/(V0 cosθ) ………….. (3)
Replacing t in equation 2 with the expression of t from equation 3:
y = (V0sinθ ). x/(V0 cosθ) – (1/2) g [ x/(V0 cosθ)]2
or, y = (tanθ) x – (1/2) g . x2/(V0 cosθ)2………..(4)In the above equation g, θ, and V0 are constant.
So rewriting equation 4:
y = ax + bx2 where a and b are constants. This is an equation representing a parabola.
So we can say that the trajectory or motion path of a projectile is a parabola.
So once thrown at an angle (excluding the right angle) with the horizontal, a projectile will follow a curved path named Parabola.
Equation of the Trajectory of a projectile is a parabola
From equation 4 above, we get the trajectory path of a projectile as y = (tanθ) x – (1/2) g. x2/(V0 cosθ)2
As you see this can be rewritten in the form y = ax + bx2 where a and b are constants. This is again an equation that represents Parabola. Hence we can say that trajectory of a projectile will follow a curve that is represented as Parabola.

Time to reach the Maximum Height by a projectile (with derivation for class 11)
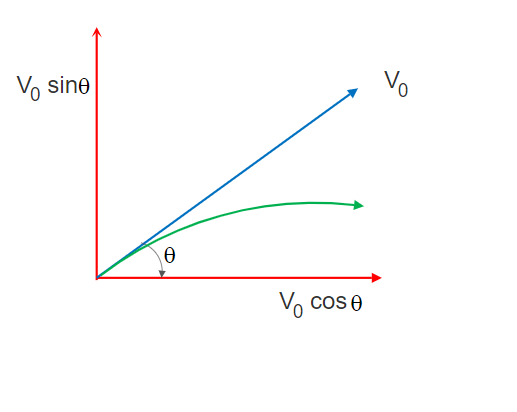
When the projectile reaches the maximum height then the velocity component along Y-axis i.e. Vy becomes 0. Say the time required to reach this maximum height is tmax.
The initial velocity for the motion along Y-axis (as said above) is V0sinθConsidering vertical motion along the y-axis:
Vy = V0sinθ – g tmax
=> 0 = V0sinθ – g tmax
=> tmax= (V0sinθ )/g ……………….(5)So this is the equation for the time required to reach the maximum height by the projectile.
Try this formula at our Projectile Motion online Calculator
Total time of flight for a projectile & Formula
So to reach the maximum height by the projectile the time taken is (V0sinθ )/g
It can be proved that the projectile takes equal time [ (V0sinθ )/g] to come back to the ground from its maximum height.
Therefore the formula of the total time of flight for a projectile Ttot = 2(V0sinθ )/g …………………. (6)
Try this formula at our Online Calculator and solve problems easily
Maximum Height reached by a projectile & Formula
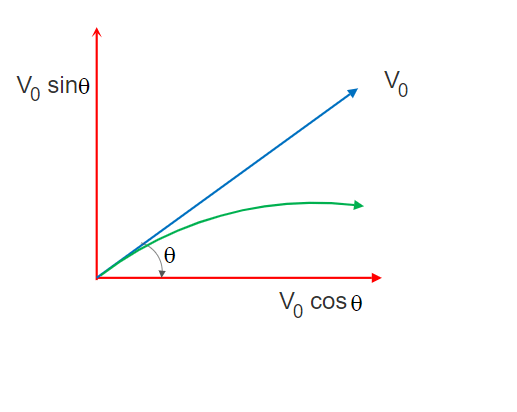
Let’s say, the maximum height reached is Hmax. We know that when the projectile reaches the maximum height then the velocity component along Y-axis i.e. Vy becomes 0.
Using one of the motion equations, we can write
(Vy)2 =( V0sinθ )2 – 2 g Hmax
=> 0 = ( V0sinθ )2 – 2 g Hmax
=> Hmax = ( V0sinθ )2/(2 g) ……………… (7) This is the equation to find the maximum height reached by a projectile.
Try this formula at our Online Calculator and solve problems easily
Horizontal range of a projectile & Formula
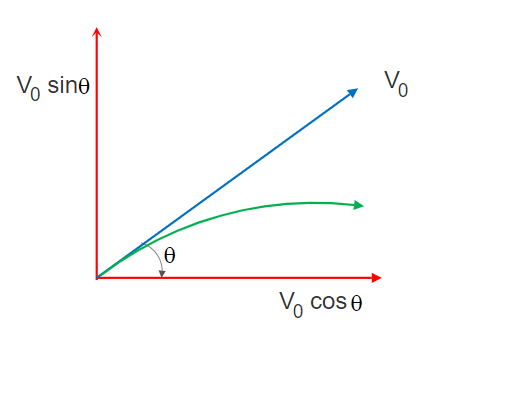
The range of a projectile is defined as the horizontal distance between the point it touches the ground and the point of projection.
Say R is the horizontal range covered by a projectile. So, R is the horizontal distance traversed by the projectile after passing the total time of flight Ttot.
[Ttot is the total time of flight.]
Here we will use the horizontal component of the initial velocity only as the effective velocity to traverse this horizontal path.
R = (V0 cosθ) . Ttot
= (V0 cosθ). 2(V0sinθ )/g = (V02 sin2θ )/ gSo the formula of the horizontal range of a projectile is R = (V02 sin2θ )/ g ………….. (8)
Note: Use our Projectile Calculator & solve problems with the formulas listed here
Greatest Horizontal Range | Maximum horizontal range (Formula derivation)
For the Maximum value of the Horizontal range, it is pretty easy to understand from the above equation that the projection angle θ needs to be equal to 45 degrees because in that case, we get the maximum value from sine as 2θ becomes 90 degrees.
Hence Maximum Horizontal Range = Rmax = V02 / g ………………….. (9)
Here we have discussed the Projectile Motion Derivation steps to derive a set of equations or formulas. We have added some numerical also in one of our posts. You should check it here: Projectile numerical problems
List of Projectile motion formulas or equations derived (In Tabular format)
| Motion Path equation: | y = (tanθ) x – (1/2) g . x2/(V0 cosθ)2 |
| Time to reach max height: | tmax= (V0sinθ )/g |
| Total time of flight for a projectile | Ttot = 2(V0sinθ )/g |
| Maximum height reached: | Hmax = ( V0sinθ )2/(2 g) |
| Horizontal range of a projectile: | R = (V02 sin2θ )/ g |
| Maximum possible horizontal range: | Rmax = V02 / g |
| At time T=t, Displacement along X-axis: | x= V0x.t = (V0 cosθ). t |
| At time T=t, Displacement along Y-axis: | y = (V0sinθ ).t – (1/2) g t2 |
State the equation of the trajectory path of the projectile
The motion Path equation can be expressed as y = (tanθ) x – (1/2) g. x2/(V0 cosθ)2
Also Read: Acceleration, velocity, displacement of projectile at different points of its trajectory
Projectile motion is a superimposed motion – an observation by Galileo
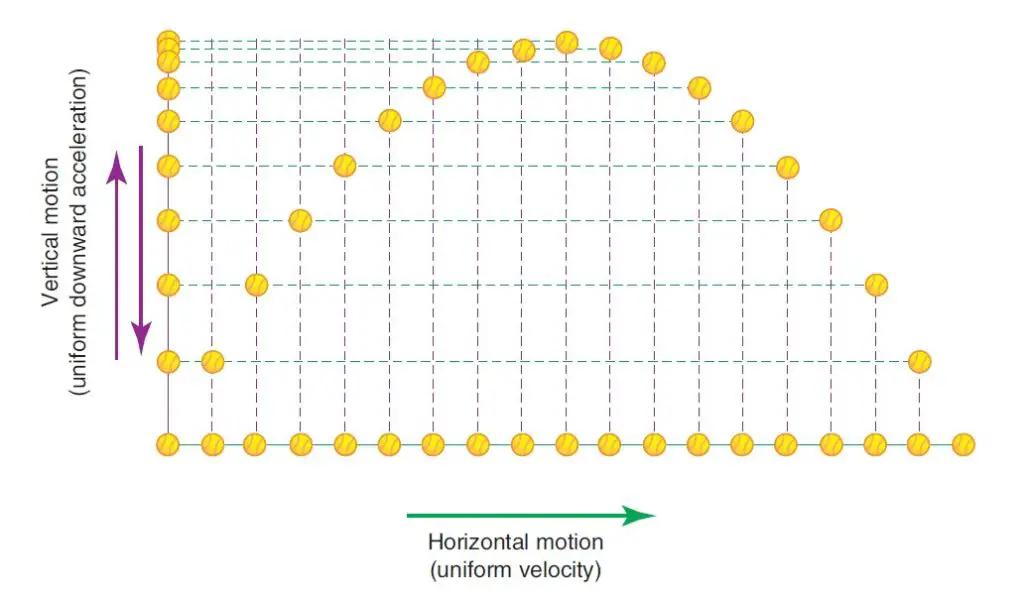
To understand and analyze projectile motion as a superimposed motion we must note an observation first made by Galileo. He observed that the motion of a projectile can be regarded as two separate and independent motions superimposed upon each other.
The first is a vertical motion, which is subject to acceleration due to gravity, and the second is a horizontal motion, which experiences no acceleration. The figure below places these two motions within a frame of reference, using the y-axis for the vertical motion and the x-axis for the horizontal motion.
Because the two motions are perpendicular and therefore independent, we can treat them separately and analyze them separately.

Formation of the parabolic trajectory of a projectile
Let us now look at how the accelerated vertical motion and the nonaccelerated horizontal motion superimpose to give the parabolic trajectory of a projectile. The figure below shows the vertical motion on the left and the horizontal motion along the base. Each successive image in both motions occurs after the same period of time. We now regard the images as time-matched pairs and use them as coordinates to plot the combined motion of the projectile. The figure below shows how this is done.
How to Calculate the velocity of the projectile at different points of its parabola trajectory?
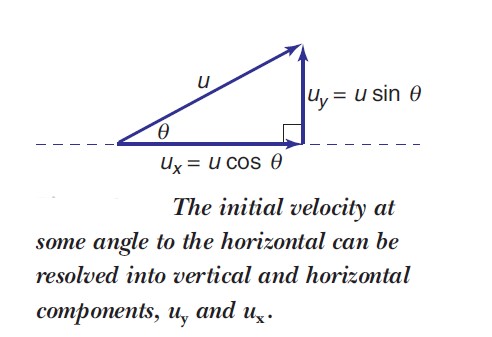
Projectiles are most commonly sent out at some angle to the horizontal. This initial velocity can quite easily be resolved into vertical and horizontal components using trigonometry, as shown in the figure below. Performing this calculation determines the initial velocity in the vertical direction and the initial velocity in the horizontal direction.
The velocity of the projectile at other times during its motion can be found by combining the vertical and horizontal velocities together in vector addition. The figure below shows how this vector addition is performed at a position where the projectile has almost risen to a peak. Notice that the real velocity of the projectile is directed at a tangent to the trajectory.

Give some real-life examples of projectile motion
A projectile is any object that is thrown, dropped, or otherwise launched into the air. This includes such things as a box dropped from a plane, a thrown ball, a struck golf ball, a kicked football, or even a fired bullet or cannonball. For our purposes, however, it does not include a rocket, because the thrust of a rocket continues well into its flight. Projectiles are projected into the air and then left to complete their unpowered flight.
When you throw some object making an angle with the horizontal (angle less than 90 degrees), and it goes off your hand then you are no more applying any force on that object. But there will be a force omnipresent acting on that stone. That is Gravity or Gravitational force applied by the earth. And this force directs vertically downwards pointing to the center of the earth. If gravity was not present that stone would continue to move in a straight line maintaining the same angle with the horizontal plane. But this downward pull of gravity takes it down.
On one hand, that stone tries to maintain a constant velocity along the horizontal as there is no force on it along that direction. On the other hand, it gets a downward pull caused by gravity and faces an acceleration equal to g (acceleration due to gravity). Under these 2 movements, it takes a parabolic path.
Force applied on a projectile and its acceleration
Throughout the flight, the projectile is subject to just one force — the force of gravity, and just one acceleration — acceleration due to gravity, g, or 9.8 m/s^2 downwards near the surface of the Earth.
Related Reading
Numerical problems on Projectile Motion.
[PDF Notes] on Projectile Motion
Equations for free fall for vertical motion
Acceleration, displacement & velocity of a projectile at different points of its trajectory
Two simple rules governing the projectile motion
- The horizontal motion and vertical motion are independent. They can be analyzed and calculated separately.
- The horizontal velocity is always constant (neglecting the air friction). The vertical motion has a constant acceleration (downward at 9.8 m/s2 at the surface of the Earth) and gravity is the only force acting on the object.

