Freefall in physics

Last updated on May 16th, 2022 at 08:53 pm

In this post we will discuss different aspects of freefall physics. Here, we will find out (a) how to find the weight of a freely falling body (b) How the velocity of a freely falling body changes every second if we ignore air drag force (air resistance)? (c) Why do we feel weightless during freefall (d) Kinetic energy of a body under free fall (e) Applicability of Law of conservation of energy for free fall (e) how distance traveled per second varies

---

---

How to find the Weight of the body during free fall?

The weight of any object is a force applied to the object by the earth’s gravitational pull towards the center of the earth.

We know the equation of a force = mass * acceleration.
i.e.      F=m*a ……. (1)

When we talk of weight force then the equation becomes like this:
Weight(W)= mass * acceleration due to gravity = m * g …… (2)

The value of g on earth is nearly 9.8 meter/second^2. This g varies a bit on different places of earth, but that’s a different story.

[read here: Acceleration due to gravity and its variation due to height and depth ]

For now, we will stick to the value given above, or for simplicity of understanding and quick calculation we may take this as 10 m/sec^2
(Note: For exam follow instructions given in your Question paper for this value on earth)

Why velocity of a freely falling body changes considering zero air resistance (ignoring air drag)?

As an object experiences free fall (considering zero air resistance), the downward force acting on it is its weight itself (mg). As we are considering zero air resistance, there is no drag force and as a result no Terminal velocity will be attained. The object will fall under the influence of a single force, i.e. Gravity.

This is caused by the earth’s pull on the object towards the center of the earth.

Under this force it’s velocity constantly rises till it touches the ground. That means the objects experiences acceleration which is known in this case as ‘Acceleration due to gravity’.

From a formula of linear motion, Current Velocity(V) = Initial Velocity (U) + Acceleration due to gravity(g)*Time elapsed (t)

V=U + gt………………………….(3)

Say a stone is being dropped from the roof of tall building. As it’s static before being dropped, so we can take the initial velocity(U) as zero.

Let’s take the  value of g as 10 in SI for simplicity of calculation.

So after 1 sec of dropping, when the stone is freely falling, it’s velocity towards downwards would be

V = 0 + 10*1 m/sec

or V=10 m/s

Again after 2 seconds of dropping, the velocity becomes,

V= 0 + 10*2 = 20 m/sec.   (Pls note that the initial velocity is 0 similar to the first case above because this velocity is the velocity of the stone before the freefall starts and as it was static at that time so we have to consider it’s value as 0 for such cases)

So it’s clear that after every second of free fall, the stone is gaining an additional velocity of 10 m/s. After 3 seconds of dropping its velocity would be 30 m/sec and after 4 seconds of dropping it will be 40 m/sec.

It’s evident that if this stone remains in the air for 10 seconds before it touches the ground then just before touching the ground its velocity would be 100 meters/second. (considering zero air resistance)

Kinetic energy is the energy possessed by a body because of its velocity. Also Read: Freefall Motion Graphs

How fast is free fall? | How much does the speed change during free fall?

The data in Table 1 below shows the instantaneous speed at the end of each second of the fall of a freely falling object dropped from rest. The elapsed time is the time that has elapsed, or passed, since the beginning of the fall. (considering g=10 m/s)

Note the Tabular speed data below to find the way the speed changes. During each second of fall, the instantaneous speed of the object increases by an additional 10 meters per second. This gain in speed per second is the acceleration and for this case, it is the acceleration due to gravity. (taken as 10 m/s^2)

Elapsed time (in seconds)	Instantaneous speed (m/s) (considering g=10 m/s)
0	0
1	10
2	20
3	30
4	40
5	50
t	10t

Here is an illustration (from CK-12) that can help in understanding the above points. (In this figure the value of g used is 9.8 m/s^2 )

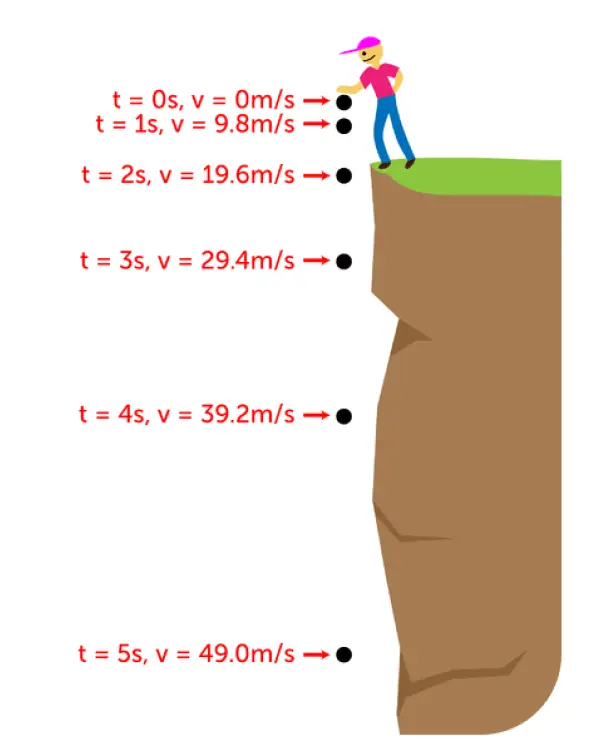
The distance traveled during free fall for every elapsed second varies -how?

Table 2 shows the total distance moved by a freely falling object dropped from rest. At the end of one second, it has fallen 5 meters. At the end of 2 seconds, it has dropped a total distance of 20 meters. At the end of 3 seconds, it has dropped 45 meters altogether. For each second of free fall, an object falls a greater distance than it did in the previous second. These distances form a mathematical pattern: at the end of time t, the object has fallen a distance d of (1/2)gt².

Elapsed time(seconds)	Distance fallen (meters)
0	0
1	5
2	20
3	45
4	80
5	125
t	(1/2)gt2

Also Read: Free fall Motion Graphs

Why feel weightless during freefall?

Here one question arises. Why does a person having a free fall (no air resistance or any drag force against his downward motion) feel weightless?

This is because the feeling of weight comes when a normal reaction force is exerted on our body by the surface on which we stand or rest.

While freefall (without any air resistance), there is no such surface that can provide this normal reaction, as a result the feeling of weight vanishes.

The person (with mass m) on freefall feels weightless as it doesn’t experience any normal reaction.. But remember that a force equal to mg is still working on him to pull him towards the center of the earth.  For details see this post. weightlessness

Kinetic Energy during free fall

Formula of Kinetic Energy (KE)= ½ mv²    

where m is the mass and v is the velocity of the body.

When a body is freely falling, at any point in time during its transit, before touching the ground it will have Kinetic Energy.

As well as it will have Potential Energy while it’s in the air due to its height from the ground.

We can show that the sum of potential energy and kinetic energy during this transit at any point will remain constant.

When air resistance is considerable and comes into play, we have to consider the air drag force which acts opposite to the weight of the falling body.

Prove that the Law of Conservation of Energy is applicable to free-fall

Say a ball of mass m is having a free fall from a height h and it finally reaches the ground with zero height.

In the diagram, the highest point is A and, the bottommost point or ground is C. B is an intermediate point.

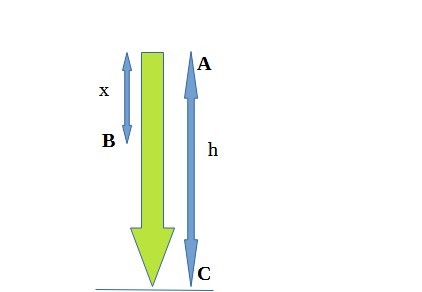
At the max height A its initial velocity=0

So at that point KE =0 and PE = mgh

So total energy at the highest point A= KE + PE = 0 + mgh = mgh

Now let’s find out the KE and PE at some point between the max height and the ground. Say that point is x distance away from the highest point. (B in the diagram) That means that the intermediate point is (h-x) distance away from the ground. At that point gravitational Potential Energy (PE) = mg(h-x)

Now as it travels to B (x distance vertically downward from A) it gains a velocity due to its accelerated motion under gravity. Let, The velocity at B is V_x. Using the motion equation with zero initial velocity:
V_x² = 2gx

Then KE at B (x distance from max height) = (1/2)mV_x² = (1/2)m2gx = mgx

So, at B = KE + PE = mgx + mg(h-x) = mgh

Now at the bottommost point C, just before touching the ground, say the velocity is V_f . At that point vertical distance traversed is h.

Again we will use one motion equation with initial velocity considered as zero(at height h velocity was zero)
V_f² = 2gh
So KE at the ground level C is =(1/2)m V_f² = (1/2)m 2gh=mgh

PE at ground level C is zero. (as height has become zero)

So the total energy at C = KE + PE =mgh + 0 = mgh

So this shows that at all 3 different points of free fall the total energy is the same and constant. This agrees with the Law of conservation of energy.

Relevant post you must read: Free Fall against air drag