Vertical motion when a ball is thrown vertically upward with derivation of equations

Last updated on May 17th, 2023 at 12:41 pm

Upward movement and then a downward movement of a ball when a ball is thrown vertically upward – this is what we will discuss here and as well as we will derive the equations of the vertical motion. So Let’s start with the fundamentals of vertical motion Kinematics.

What happens when a ball is thrown vertically upward?

When a ball is thrown vertically upward it starts its vertical motion with an initial velocity.
As it moves upwards vertically its velocity reduces gradually under the influence of the earth’s gravity working towards the opposite direction of the ball’s motion.

In other words, during upward movement, the ball is moving with retardation. And finally, the velocity of the ball becomes zero at a height.

Then again it starts falling downwards vertically and this time its velocity increases gradually under the influence of gravity. During downward movement ball’s direction is the same as that of gravity and as a result, the ball comes down with acceleration and reaches the ground.

What are the important formulas or pointers related to vertical motion?

The important formulas and pointers for vertical motion include
1> The maximum height reached,
2> Time required for up & down movement,
3> Acceleration of the ball at different points,
4> The velocity of the ball at different instances,
5> Forces acting on the ball,
6> Formula or equation of vertical motion
7> Kinetic energy and potential energy of the ball in a vertical motion

We will find all these in this post. Let’s discuss the phases of this traversal and motion with some formulas and examples.

What is the equation for an object thrown upward?

The motion equations applicable for an object thrown upward are:
During upward movement:
V = U – gt………(i)
H =Ut – (1/2) g t²…….(ii)
V² = U² – 2gH…..(iii)
During downward movement:
V = U + gt………(iv)
H =Ut + (1/2) g t²…….(v)
V² = U²+ 2gH…..(vi)

List of formulas related to a ball thrown vertically upward [formula set]

If a ball is thrown vertically upwards with an initial velocity of U then here is a set of formulas for your quick reference.
1) Maximum height reached H_max = U² / (2 g)
2) Velocity at the highest point = 0
3) Time for upward movement = U /g
4) Time for downward movement = U /g
5) Total time of travel in air = (2 U )/g
6) Acceleration of the ball = acceleration due to gravity (g) acting downwards, towards the center of the earth [ignoring air resistance]
7) Forces acting on the ball = Gravity (gravitational force exerted by the earth)
[ignoring air resistance]

Numerical Problems – to solve using Vertical motion formulas

A ball is thrown vertically upwards with a velocity of 49m/s calculate the maximum height and time taken to reach maximum height.

H = U²/(2g) = (49²)/(2 x 9.8)=122.5 m
T = U/g = 49/9.8 = 5 sec

A ball is thrown vertically upward with a velocity of 20 m/s. calculate the maximum height and time taken to reach maximum height.

H = U²/(2g) = (20²)/(2 x 9.8)=20.4 m
T = U/g = 20/9.8 = 2.04 sec

A ball is thrown vertically upwards. it returns 6s later. The velocity with which it was thrown is:

The time taken to reach its max height = 6/2 = 3 sec
We know, T = U/g
or, U = gT
U= 10 x 3 m/s = 30 m/s

Upward movement of the ball when a ball is thrown vertically upward – some important points

Say a ball is thrown vertically upward with some velocity say v1, which we will consider as the initial velocity for the upward path.

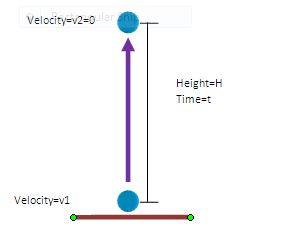
After a certain time period t, the ball reaches a height beyond which it can’t move upwards anymore and stops there i.e. its velocity becomes zero at that height.

The height where the velocity becomes zero which is the maximum height the ball went upward, say is H.

And for this upward movement, the final velocity v2 is 0 because the ball has stopped at the end of this upward traversal.

Why does an object thrown upwards come down after reaching a point?

When an object is thrown with a certain initial velocity (say V), it gains Kinetic energy at that moment of throwing. As it moves upwards from its initial position (wherefrom it’s thrown) and gains height, its potential energy rises. This happens because Potential Energy (PE) is directly proportional to the height of the object. (PE = mgh where h is the height).

Now from the Law of conversation of energy, we can say this rise in PE is happening at the cost of some form of energy being transformed.

Here it’s the kinetic energy of the object which is expressed as (1/2)mV². As height rises, velocity falls which results in a reduction of KE and a corresponding rise in PE. At one point KE becomes zero. At that point, velocity becomes zero. This is called the highest point for an upward vertical movement. After this, the ball starts falling downwards.

Differently, we can say that the KE availed by the thrown object gets corroded under the negative influence of oppositely directing gravity (Gravitational force due to earth).

The influence is negative because gravity is pulling downwards while the ball is trying to move upwards. After some time when the entire KE gets nullified, the ball stops. And then starts falling towards the earth’s surface.

In all the above discussions, we have considered Air Resistance as negligible.

**Those who are aware of escape velocity, can read a post on it here: Escape Velocity

What are the forces acting on a ball thrown upwards?

Considering the Air resistance or Drag force negligible, the only force acting on the ball is Gravity i.e. the Gravitational Pull of the earth towards the center of it.

What is the acceleration of a ball thrown vertically upward during upward movement?

The acceleration of the ball would be equal to the acceleration due to gravity caused by gravitational pull or force exerted by the earth on the ball. Its value is approximately 9.8 m/s^2 and its direction would be downwards towards the center of the earth.

It’s pretty evident that after the upward throw, the velocity of the ball gradually decreases i.e. a negative acceleration was working on the ball. The acceleration is negative because this acceleration is directing downwards while the ball is moving upward.

And because of this negative acceleration, the velocity of the ball is gradually decreasing. And Yes. As said above, this acceleration is nothing but the acceleration due to gravity caused by gravitational pull or force exerted by the earth on the ball. Its value is generally taken as 9.8 m/s^2.

See here how acceleration due to gravity varies with height and depth wrt the surface of the earth.

Derive the equation of the Time taken by the ball to reach the maximum height during its upward movement

As this acceleration due to gravity (g) is working opposite to the upward velocity we have to use a negative sign in the formula below, used for the upward movement of the ball.

We know the value of g in SI is 9.8 m/second square.

Using one of the equations of motion,

v2  = v1  –  gt ……………………(i)

As v2=0, (at the highest point the velocity becomes zero), then we can write the previous equation as follows:

  0  =  v1  –  gt

or, t  =  v1/g …………………….(ii)

So from equation (ii), the time taken by the ball to reach the maximum height = (Initial Velocity with which the ball is thrown vertically upwards) / (acceleration due to gravity)…..(iii)

So just for example, if a ball is thrown vertically upwards with 98 m/s velocity, then to reach the maximum height it will take = 98/9.8 =10 seconds.

Derive the formula for the maximum height reached during upward movement when a ball is thrown vertically upward.

And the maximum height H reached is obtained from the formula:

v2²=v1²-2gH     ( under negative acceleration)  ……………… (iii)

As v2=0, (at the highest point the velocity becomes zero), so we can rewrite equation iii as:

0 = v1² – 2gH

or  H= v1²/2g (equation of maximum height)     ………. (iv)

Therefore if a ball is thrown vertically upwards with 98 m/s velocity, the maximum height reached by it would be = (98 x98 )/(2 x 9.8) meter = 490 meters.

What is the velocity of the ball when it reaches the highest point?

Just summing up the answer here though we have already gone through this in the section above.

The velocity at the highest point is zero as the ball momentarily halts there before starting its downward movement.

What is the acceleration of the ball when it reaches the highest point?

And the acceleration working on the ball at this point is the acceleration due to gravity (g). At this highest point, the ball is all set to fall vertically downwards with acceleration g. During this free fall (ignoring air resistance), g is used with a positive sign in motion equations.

Downward movement of the ball

And finally, the velocity of the ball becomes zero at a height.

At the highest point of the upward motion, the ball starts falling downwards vertically and this time its velocity increases gradually under the influence of gravity.

During downward movement ball’s direction is the same as that of gravity and as a result, the ball comes down with acceleration and reaches the ground.

What is the acceleration of a ball thrown vertically upwards during its downward movement?

As the ball reaches the maximum height now it starts its free-fall towards the earth. The force applied to it is again gravity and this time it’s having a positive acceleration i.e. it’s following the same direction of the acceleration due to gravity (g)

What is the velocity of the ball just before touching the ground?

 And one important point, during the downward fall the magnitude of the velocity of the ball just before touching the ground would be the same as the magnitude of the velocity with which it was thrown upwards (v1 here). We will prove it mathematically here:

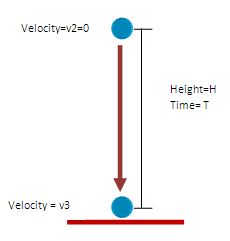
Here while falling vertically downward, the ball falls the same height H (here H = v1²/2g,  as given in equation iv)

During this downward displacement, the initial velocity is equal to the final velocity of the upward movement i.e. v2. And we know that v2=0.

And during the downward movement, the final velocity is v3. This velocity is attained by the vertically falling ball just before touching the ground.

We have to find out the expression of this v3. Also, we have to find out the time taken (say T) for this downward fall.

v3² = v2² + 2 g H = 0 + 2 g (v1²/2g) = v1²
i.e. v3 = v1…………….(v)

So we can say that during the downward fall the magnitude of the velocity of the ball just before touching the ground would be the same as the magnitude of the velocity with which it was thrown upwards (v1 here).

Find out the formula of the time period for the downward movement when a ball is thrown vertically upward

It can be proved that the time for the downward movement or the time taken by the ball to fall from the highest point and reach the ground is same as the time required for the upward movement =  v1/g

Let’s prove it here mathematically:
(see the diagram above for downward movement)

v3 = v2 + g T
or,   v3 = 0 + g T

so,   T = v3/g = v1/g  (from equation v above) ………….(vi)

So Time for downward movement (T) = Time for upward movement ( t ) = v1/g

That means, time for downward travel = time of upward travel

Total time required for the upward and downward movement [Total time of flight]

So (from equations ii and vi) for a vertically thrown object the total time taken for its upward and downward movements = t + T=2v1/g ……….(vii)

A complete case study:

Say a ball is thrown vertically upward with 98 m/s velocity, So v1 = 98 m/s

1) The maximum height reached by it would be = v1²/2g= (98 x98 )/(2 x 9.8) meter = 490 meter.

2) The time taken to reach the highest point = v1/g = 98 / 9.8 second = 10 second

3) The velocity at the highest point = 0

4) The time taken to reach the ground while falling from the highest point = v1/g = 98 / 9.8 second = 10 second

5) Total time taken for upward and downward movement = 10 sec + 10 sec = 20 sec.

6) Velocity just before touching the ground=same as initial velocity of throwing = 98 m/s

Suggested & Related Post 

 Share Now:

Hope you have enjoyed this post. Now you may share it as much as possible using the social media buttons on the page.