Acceleration, velocity, and displacement of projectile at different points of its trajectory
Last updated on December 3rd, 2022 at 02:49 pm
Acceleration, velocity, and displacement of the projectile at different points of its parabolic trajectory are what we are going to study here. Both horizontal and vertical components of these 3 motion quantities will be presented in tabular format.
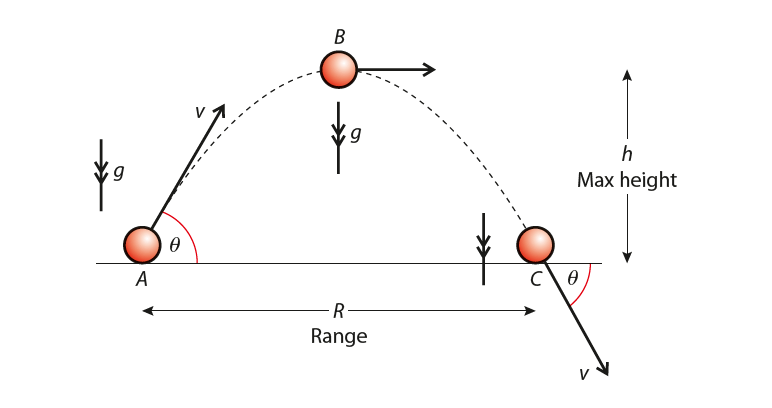
Consider a ball that is projected at an angle θ to the horizontal with velocity v, as shown in Figure 1. R is the horizontal range. We can split the motion into three parts, beginning, middle, and end, and analyze the vectors representing displacement, velocity, and time at each stage.
Note that since the path is symmetrical, the motion on the way down is the same as the way up.
We can see that the vertical motion is constant acceleration and the horizontal motion is constant velocity.
Horizontal components of displacement, velocity, and acceleration of a projectile
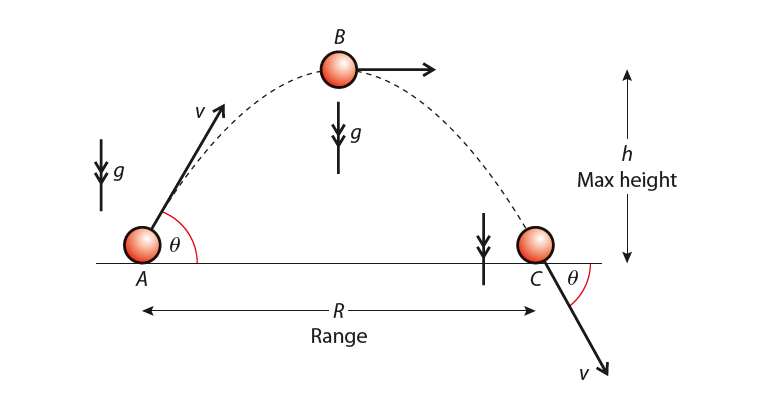
Consider a ball that is projected at an angle θ to the horizontal with velocity v, as shown in Figure 2.
R is the horizontal range.
At A (point of projection) the horizontal displacement is zero, the horizontal velocity is v cos θ and the horizontal acceleration is 0.
At B (highest point of trajectory) the horizontal displacement is R/2, the horizontal velocity is v cos θ and the horizontal acceleration is 0.
And at C (the last point of the trajectory) the horizontal displacement is R, the horizontal velocity is v cos θ and the horizontal acceleration is 0.
These are presented in table 1 below. Refer to figure 2 while going through the table data.
We can easily say that horizontal motion is constant velocity.
| At A (time = 0) | At B (time = t /2) | At C (time = t) |
|---|---|---|
| Displacement = zero | Displacement = R/2 | Displacement = R |
| Velocity = v cos θ | Velocity = v cos θ | Velocity = v cos θ |
| Acceleration = 0 | Acceleration = 0 | Acceleration = 0 |
Vertical components of displacement, velocity, and acceleration of a projectile
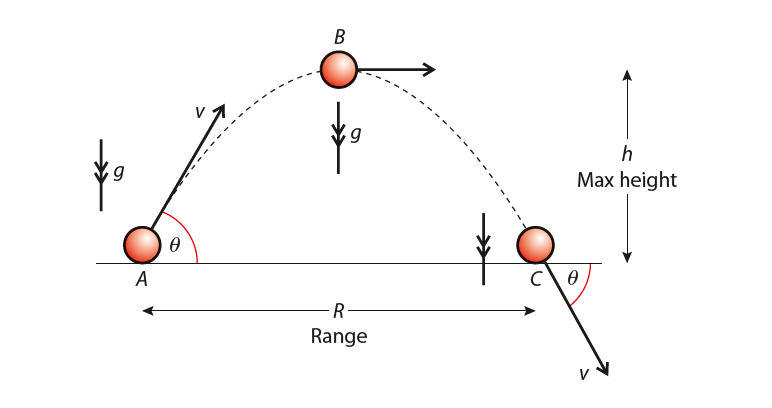
Consider a ball that is projected at an angle θ to the horizontal with velocity v, as shown in Figure 3.
R is the horizontal range.
At A (point of projection) the vertical displacement is 0, the vertical velocity is v sin θ and the vertical acceleration is -g.
At B (highest point of trajectory) the vertical displacement is h, the vertical velocity is 0 and the vertical acceleration is -g.
And at C (the last point of the trajectory) the vertical displacement is 0, the vertical velocity is -v sin θ and the vertical acceleration is -g.
These are presented in table 2 below. Refer to figure 3 while going through the table data.
We can see easily that the vertical motion is constant acceleration.
| At A (time = 0) | At B (time = t /2) | At C (time = t) |
|---|---|---|
| Displacement = zero | Displacement = h | Displacement = 0 |
| Velocity = v sin θ | Velocity = 0 | Velocity = -v sin θ |
| Acceleration = -g | Acceleration = -g | Acceleration = -g |
Also read: derivation of the projectile equation & important FAQs
At the highest point of the trajectory, what is the acceleration of a projectile?
The acceleration of the projectile at the peak is -g. g denotes the acceleration due to gravity (9.81 m/s^2).
The minus sign indicates that the direction of acceleration of the projectile at the highest point of trajectory is opposite to the positive Y-axis, i.e. its direction is towards the earth. g denotes the acceleration due to gravity.
[Note: At the highest point, the horizontal component of the acceleration is zero, and the vertical component of acceleration is -g. ]
Vertical motion is constant acceleration for a projectile – how?
The vertical component of acceleration remains constant at -g during the entire trajectory of the projectile. Hence, the vertical motion of a projectile is constant acceleration.
Also read: Numerical problems on projectile motion
Horizontal motion is the constant velocity for a projectile – how?
The horizontal component of the acceleration of the projectile is 0 and hence the projectile maintains a constant velocity in its horizontal motion.
What is the velocity of a projectile at the peak of its path?
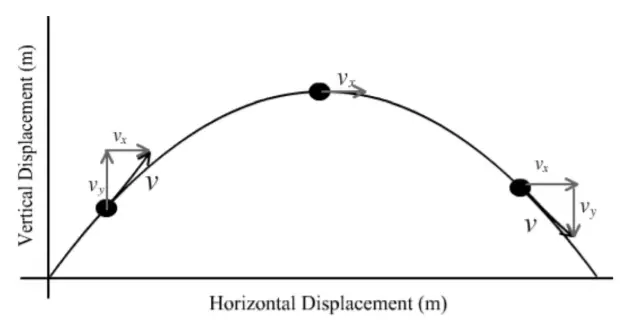
At the top of its flight, when the object stops rising and is about to fall, the vertical speed of an object is zero. The horizontal speed at that point is expressed as v cos θ.
(Considering that it is projected at an angle θ to the horizontal with velocity v.
Refer to figure 4)
Related:
1> derivation of the projectile equation & important FAQs
2> Numerical problems on projectile motion
