Time of flight equation for projectile

The equation of the total time of flight for a projectile is T_tot = 2(V₀sinθ )/g

Time of flight equation – derivation

To derive the time of flight equation of a projectile we first have to find out the time to reach the Maximum Height by a projectile.

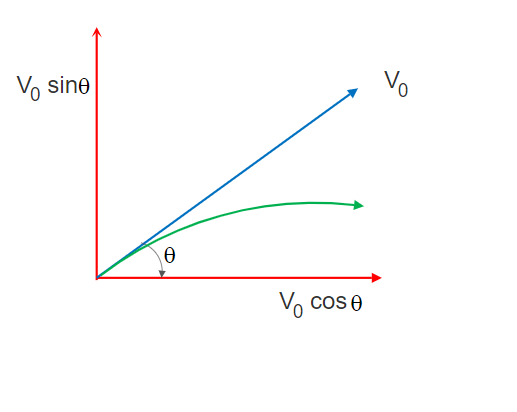
When the projectile reaches the maximum height then the velocity component along Y-axis i.e. V_y becomes 0. Say the time required to reach this maximum height is t_max.
The initial velocity for the motion along Y-axis (as said above) is V₀sinθ

Considering vertical motion along the y-axis:

V_y = V₀sinθ  – g t_max ………………….. (1)

At the maximum height. equation 1 becomes:
=> 0 = V₀sinθ  – g t_max

=> t_max= (V₀sinθ )/g     ……………….(2)

So this is the equation for the time required to reach the maximum height by the projectile.

So to reach the maximum height by the projectile the time taken is  (V₀sinθ )/g

It can be proved that the projectile takes equal time [ (V₀sinθ )/g] to come back to the ground from its maximum height.

Therefore the formula of the total time of flight for a projectile T_tot = 2(V₀sinθ )/g …………………. (3)