Prove that projectile motion is parabolic class 11

Here we will Prove that projectile motion is parabolic (class 11). To do this we need to derive the Projectile Motion Path Equation (or Projectile trajectory equation) first.

Projectile motion is parabolic – let’s prove this (class 11)

Say an object is thrown with uniform velocity V₀ making an angle θ with the horizontal (X) axis.

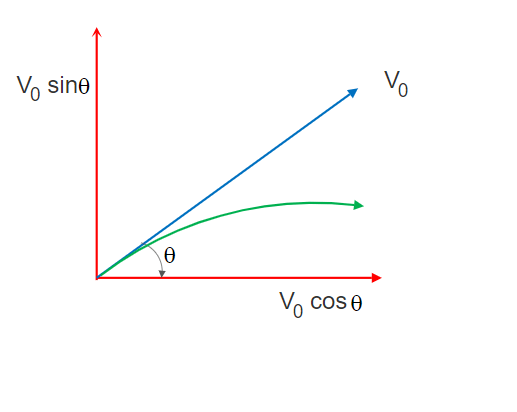
The initial velocity component along the horizontal X-axis = V_0x = V₀ cosθ
And the initial velocity component along the vertical Y-axis = V_0y = V₀sinθ.
(Air resistance is taken as negligible)

At time T = 0, there is no displacement along the X and Y axes.

At time T=t, (i.e., for any time instant t)
Displacement along X-axis = x= V_0x.t = (V₀ cosθ). t ………… (1) and
Displacement along Y-axis = y = (V₀sinθ ).t  – (1/2) g t² …………(2)

From equation 1 we get: t = x/(V₀ cosθ) ………….. (3)

Replacing t in equation 2 with the expression of t from equation 3:

y = (V₀sinθ ). x/(V₀ cosθ)  – (1/2) g  [ x/(V₀ cosθ)]² 
or, y = (tanθ) x –   (1/2) g . x²/(V₀ cosθ)²………..(4)

In the above equation g, θ, and V₀ are constant.

Let’s rewrite equation 4:
y = ax + bx² where a and b are constants.
This is an equation representing a parabola.

So we can say that the trajectory or motion path of a projectile is a parabola. And, projectile motion is parabolic.
So once thrown at an angle (excluding the right angle) with the horizontal, a projectile will follow a curved path named Parabola.