Equation of Trajectory of a Projectile

The equation of the trajectory of a projectile shows that this trajectory path represents a parabola. This means that a projectile follows a parabolic path.

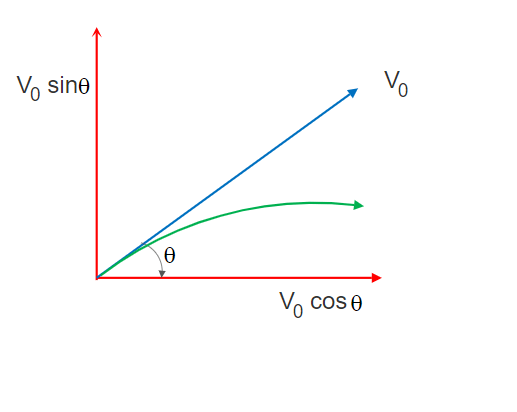
Equation of Trajectory of a Projectile

Referring to Figure 1 above, we can calculate and get the trajectory path of a projectile as follows.
Equation of Trajectory of a Projectile: y = (tanθ) x – (1/2) g. x²/(V₀ cosθ)²

As you see this can be rewritten in the form y = ax + bx² where a and b are constants.
This is again an equation that represents Parabola.

Hence we can say that trajectory of a projectile will follow a curve that is represented as Parabola.

Deriving the Equation of the Trajectory of a Projectile

Referring to Figure 1 above, the initial velocity component along X-axis = V_0x = V₀ cosθ and the initial velocity component along Y-axis = V_0y = V₀sinθ.
(Air resistance is taken as negligible)

At time T = 0, there is no displacement along the X and Y axes.

At time T=t, (i.e., for any time instant t)
Displacement along X-axis = x= V_0x.t = (V₀ cosθ). t ………… (1) and
Displacement along Y-axis = y = (V₀sinθ ).t  – (1/2) g t² …………(2)

From equation 1 we get: t = x/(V₀ cosθ) ………….. (3)

Replacing t in equation 2 with the expression of t from equation 3:

y = (V₀sinθ ). x/(V₀ cosθ)  – (1/2) g  [ x/(V₀ cosθ)]² 
or, y = (tanθ) x –   (1/2) g . x²/(V₀ cosθ)²………..(4)

In the above equation g, θ, and V₀ are constant.

So rewriting equation 4:
y = ax + bx² where a and b are constants. This is an equation representing a parabola.
So we can say that the trajectory or motion path of a projectile is a parabola.
So once thrown at an angle (excluding the right angle) with the horizontal, a projectile will follow a curved path named Parabola.