Electric flux – definition, formula
Last updated on June 19th, 2022 at 01:28 pm
Electric flux – definition, formula – In this post, we will define electric flux and study its equation. We will also study a few figures that come with numerical problems related to electric flux. Later, we will find the statement of Gauss’ theorem.
Electric Flux – definition
Definition of flux: The total number of electric field lines crossing a surface normally is called electric flux.
Electric flux can also be defined as the surface integral of the Electric Field over the entire closed surface.
Electric Flux equation | formula of electric flux
Formula or equation of electric flux: The electric field through surface element dS is ΔΦ = E.dS = E dS cos θ, where E is the electric field strength. (see figure 1)
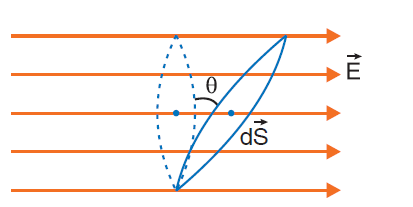
The surface integral form of the flux formula is this: ΦE = ʃA E. ds
This can be expanded as ΦE = ʃA E. ds = ʃA E ds cos θ = ES cos θ
When, θ = 0° i.e., when the area vector and the electric field vector are parallel, then ΦE = ES
Here, S = surface area.
[ Note: The area vector is normal (perpendicular) to the surface]
θ in the electric flux equation
θ is the angle between the direction of the Electric field E and the normal to the surface being considered.
In other words, θ is the angle between the direction of the Electric field E and the area vector.
[ Note: The area vector is normal (perpendicular) to the surface]
How to quickly find this θ from a given figure or diagram when solving numerical problems?
θ = the minimum angle by which we have to rotate the surface plane to make it normal to E field line direction= minimum angle by which we have to rotate the E field line direction to make it normal to the Surface.
We will do this quick check because the definition of flux considers only the electric field lines crossing a surface normally. [normal means perpendicular]
finding flux from figures
See figure 2.
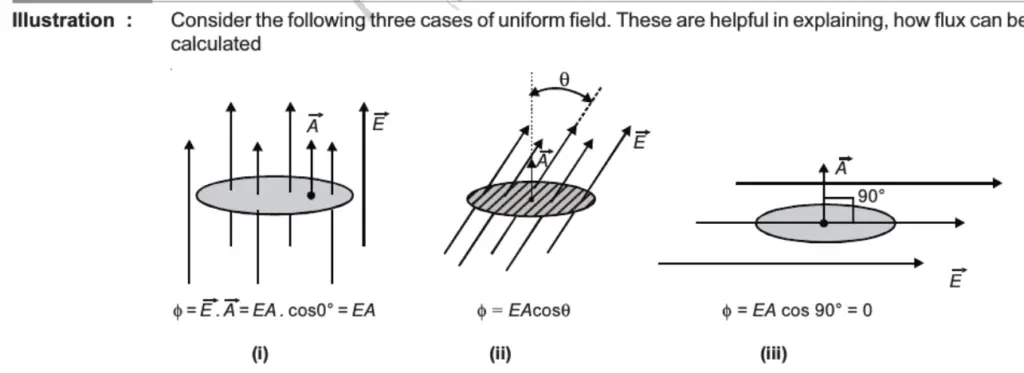
flux In figure 2 (i):
θ = angle between the direction of the Electric field E and the normal to the surface being considered = 0°.
In other words, the minimum angle by which we have to rotate the E field line direction to make it normal to Surface = 0°.
Hence, flux Φ = E . A = EA cos 0° = EA
flux In figure 2 (ii):
θ = angle between the direction of the Electric field E and the normal to the surface being considered.
In other words, minimum angle by which we have to rotate the E field line direction to make it normal to Surface = θ
Hence, flux Φ = E . A = EA cos θ
flux In figure 2 (iii):
θ = angle between the direction of the Electric field E and the normal to the surface being considered = 90°.
In other words, minimum angle by which we have to rotate the E field line direction to make it normal to Surface = 90°.
Hence, flux Φ = E . A = EA cos 90° = EA
Gauss’s Theorem statement
It states that the total electric flux through a closed surface is equal to 1/ε0 times the net charge enclosed by the surface.
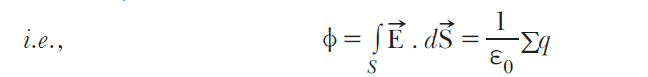
Also read: Derivation of Gauss’ Theorem
