Electric Field – Formula, direction & derivation
Last updated on July 5th, 2022 at 09:44 pm
A space that causes charged particles to accelerate is said to have an Electric Field. By definition, the electric field (E) at a given point in the space surrounding a source charge is the ratio of the electric force (F) exerted on a test charge (q) placed at that point to the magnitude of that charge. In other words, Electric field strength, E, is defined as the force per unit positive charge. It’s the force that a charge of +1 C would experience if it was placed in the electric field.
The electric field can be calculated using the equation E = F/q where q is the magnitude of the test charge in coulombs (C); F is the electric force on the test charge applied by the source charge in Newton (N), and E is the strength of the electric field at that point in Newton per coulomb (N/C).

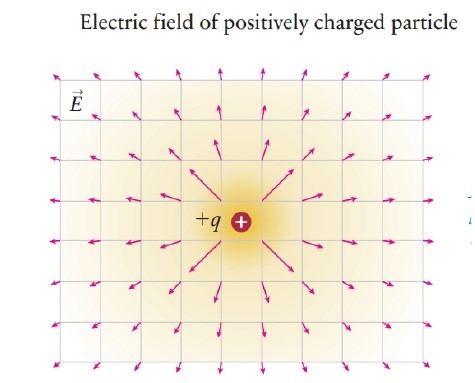
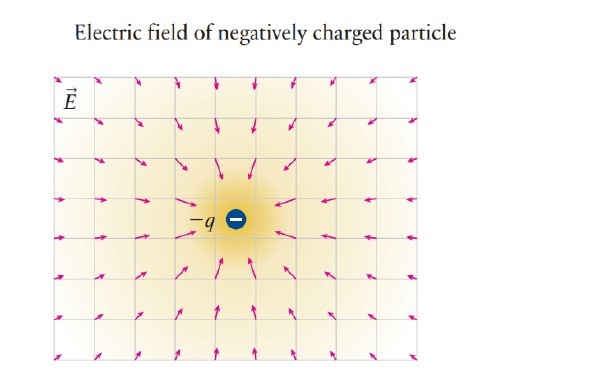
The direction of the electric field at a point is the direction of the electric force exerted on a positive test charge at that point. (a) If the source charge is negative, the field is directed toward the source. (b) If the source charge is positive, the field is directed away from the source.
The electric field is a vector quantity. Electric fields are represented by electric field lines. An electric field line indicates the direction in which a positive test charge would move if placed at a point in the electric field.
The electric field (symbol E) is defined as the electric force per unit charge: E = F/q, measured in SI units Newton per Coulomb (N/C). The term Electric Field is also known as Electric Field Strength.
- Electric Field and its direction
- Properties of electric field lines
- Equation or formula of Electric Field | Magnitude of electric field
- Direction of the Electric Field
- Derivation of the Electric Field equation using Coulomb’s law
- Superposition principle to get the resultant electric field caused by more than one charges
- Direction of the Electric Field for a pair of metal plates with opposite charge distribution
- Lines of force
- Representing electric fields with a diagram
- Electric Force formula from the Electric Field formula
- Formula of the acceleration of the charge in an Electric Field
- Electric Potential definition and Formula
- Potential Difference | Kinetic Energy gained by a charged particle
- Summary
Electric Field and its direction
Coulomb’s law gives the force between two charges. But practically when we have millions of charges it’s quite impractical to use Coulomb’s law to find the net force on any single charge. In situations like this, the concept of a field to describe how the electric force acts on charges becomes useful.
An electric field surrounds a charge and represents the physical effect of a particular charge in a nearby space. When another charge is placed in the field, the field will exert an electric force on that charge.
You can imagine determining or mapping out an electric field by using a small positive charge (a test charge) at a location near the charge of field interest. The force (magnitude and direction) on the test charge is recorded. The electric field (E = F/q) is the force per unit charge.
In this manner, if an arbitrary charge q is placed in the field E, then the magnitude of the force on it can be found by F = q E, with the direction depending on the sign of the charge or how it would react to a positive test charge.
When the electric force is determined at many locations, we have a vector “map” of the electric force field.
We can understand the electric field concept with a more familiar example of gravity.
We know that if we drop an object from some height above the earth’s surface, it experiences the force of gravity and begins to fall. We can think of the space above Earth as having a gravitational field that will generate a force on any object we place there.
In this case, you’d define the gravitational field to have a value g = F/m, or the force per unit mass on the object. The field’s direction is downward, toward Earth. The electric field (symbol E) is defined in a similar way, as the electric force per unit charge: E = F/q
Properties of electric field lines
Electric field lines:
- start and end perpendicular to the surface of a charged object
- never cross each other
- are closer where the electric field is stronger
- are directed from positive to negative
Equation or formula of Electric Field | Magnitude of electric field
The electric field (symbol E) is defined as the electric force per unit charge and is expressed with the equation as follows: E = F/q, where F is the force applied by the source charge on the test charge and q is the magnitude of that test charge.
Let’s see how the electric field equation can be expressed for (1) radial electric field & (2) Uniform electric field.
In a Radial Field, E is Inversely Proportional to r2
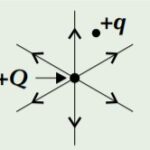
For a positive Q, a small
positive ‘test’ charge q would
be repelled, so the field lines
point away from Q.
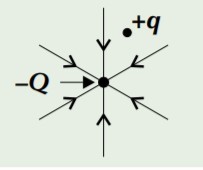
For a negative Q, a small
positive charge q would be
attracted, so the field lines
point towards Q.
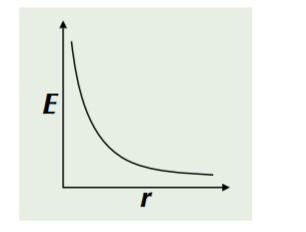
In a radial field, the electric field strength, E, depends on the distance r from the point charge Q:
E = kQ / r2 where constant k = 1/(4πε0)
And, E is the electric field strength (N/C), ε0 is the permittivity of free space (8.85× 10-12 Farad/m), Q is the point source charge (C) and r is the distance from the point charge (m).
Field strength decreases as you go further away from Q.
A graph of E against r looks like this:
In a Uniform Field, E is the Same Everywhere
1) A uniform field can be produced by connecting two parallel plates to the opposite poles of a battery:
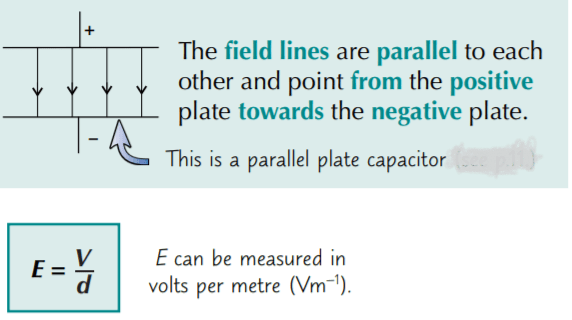
2) In a uniform field, the field lines are parallel so they’re always the same distance apart. This means that the field strength is the same at all points within the field — i.e. a test charge would experience the same force wherever it was.
3) The field strength between two parallel plates depends on the potential difference between the plates, V, and the distance, d, between them, according to the equation: E = V/d
Direction of the Electric Field
The direction of the electric field at a location is the same as the direction of the electric force on a positively charged particle at that location in the field.
i.e. Direction of the electric field = Direction of the force on a positively charged particle.
As said earlier that the direction of the electric field at a point is the direction of the electric force exerted on a positive test charge at that point. Therefore, (a) If the source charge is negative, the field is directed toward the source. (b) If the source charge is positive, the field is directed away from the source.
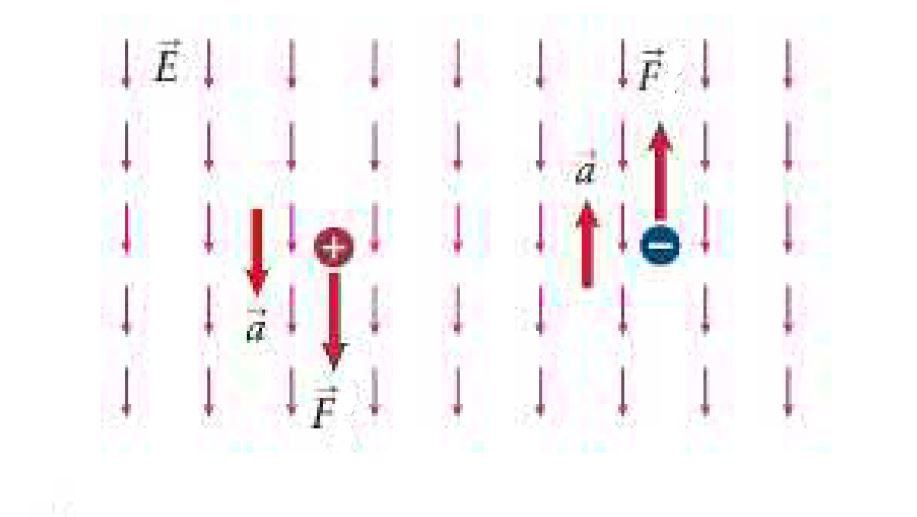
Obviously, the electric force on a negative particle is directed opposite to the electric field.
Figure (3) below shows forces exerted by a uniform electric field on positively and negatively charged particles. Here evidently the source charge is positive.
Derivation of the Electric Field equation using Coulomb’s law
As per Coulomb’s Law, the electric force on a test charge q applied by the source charge Q can be expressed as:
F = (k Qq)/r2 ………..(equation 1), where r is the distance between the two charges.
Now if there is electric field E at that specific location where charge q rests then we can write the equation of the electric force applied on q in this way as well:
F = E q ………………(equation 2)
Now as these 2 equations express the same electric force, we can easily write:
E q = (k Qq)/r2
=> E = (k Q)/r2 …………….. (This is the equation of the electric field at a distance r from the source charge Q)
If the source charge Q is positive then the electric field E is positive and the direction of the electric field E will be radially outward from Q. And if the source charge Q is negative then the electric field E is negative and its direction will be radially inward.
Superposition principle to get the resultant electric field caused by more than one charges
The Net Electric Force applied on a test charge by n number of source charges can be obtained by the superposition principle where the net force is the vector sum of the individual electric forces being applied on the test charge by the individual source charges.
Similarly, the net Electric field at a location in space can be obtained by the superposition principle where the net electric field is the vector sum of all the individual electric fields due to individual electric charges.
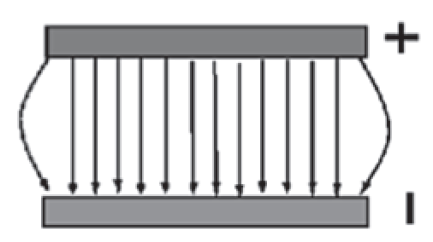
Direction of the Electric Field for a pair of metal plates with opposite charge distribution
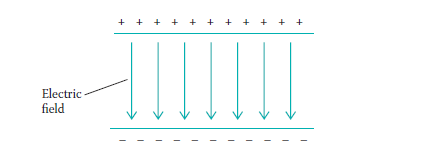
The figure above shows a good way to make a fairly uniform electric field:
Let’s consider the distribution of opposite charges (positive and negative) on a pair of parallel metal plates.
As we said earlier, the direction of the electric field is determined by the direction of the force on a positively charged particle. So in the case of pair of parallel metal plates with opposite charge distribution, we have to note the direction of the force on the positively charged particles.
In this case, the direction of the force on the positively charged particles is along the direction represented with arrows (in the diagram above).
Hence the electric field will also be the same as the direction represented with arrows between the plates i.e. from the positive plate to the negative plate.
The strength of the field depends on how much charge we put on the plates—more charge makes a stronger field, consistent with Coulomb’s law.
SI unit of electric field
SI unit is Newton per Coulomb (N/C)
Lines of force
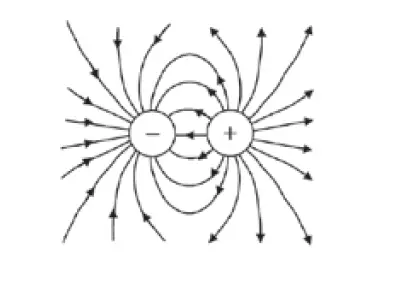
When the field vectors are connected, we have lines of force, where the arrowheads indicate the force direction on a positive charge. If an arbitrary charge were put in a field and released, it would follow one of these lines, the field acting on the charge.
The lines between the positive and negative charges begin and end on the charges, respectively. This indicates that the charges are attractive, and the field gets stronger as the lines of force get closer.
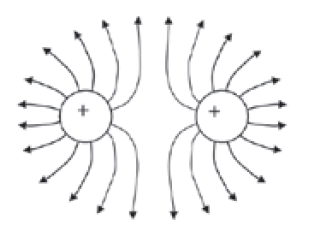
For the two positive charges (or two negative charges), there are no lines of force between them, which indicates that the charges are repulsive.
Representing electric fields with a diagram
Here is a list of simple diagrams to show the electric fields around charged objects:
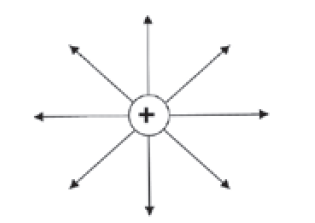
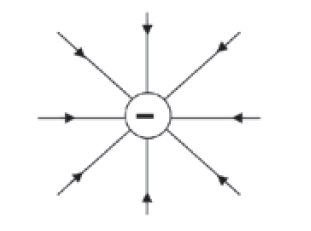
negative). If the point charges are negative, the arrows point inwards, towards the point charges.
equally spaced and parallel.
Electric Force formula from the Electric Field formula
The electric field is expressed with the equation E = F/q where q is the magnitude of the test charge in coulombs (C); F is the electric force on the test charge applied by the source charge in Newton (N), and E is the strength of the electric field at that point in Newton per coulomb (N/C).
Now from this equation of E, we can easily get the equation or formula of the Electric Force F.
Electric Force = F = E q
This means the electric force that acts on a charged particle is calculated by multiplying the Electric Field Strength(E) with the amount of charge q.
Formula of the acceleration of the charge in an Electric Field
The equation or formula of the Electric Force F acting on a charge q placed in an electric field E is given as follows:
Electric Force = F = E q
Now we know from Newton’s 2nd law that force can be expressed as F = m a where m is the mass and a is the acceleration of the charged particle.
We can therefore write that, m a = E q
=> Hence, the formula of the acceleration of the charge in an Electric Field is as follows: a = (E q)/m
Thus we get the formula of the acceleration of the charge.
A charged particle placed in a uniform electric field undergoes constant acceleration.
Now, what’s the direction of the acceleration? If the test particle carries a positive charge (q > 0) then the electric force on it and its acceleration have the same direction as electric field E. If q < 0, Force and acceleration point towards the direction opposite the direction of the electric field.
Electric Potential definition and Formula
Every location within an Electric field gives a charged particle a certain electric potential energy. This potential energy is equal to the work done to bring that charged particle to that location within the electric field. From this, we get the concepts of electric potential.
The Electric Potential of a location within an electric field is the electric potential energy per unit of charge at that location.
The formula of electric potential(V) can be written like this: V = Ep /q where Ep denotes electric potential energy gained by the charge q. This is also written as V = W /q where W denotes the work done to move the charge q.
Here we also get the equations of work done to move a charge in an electric field and the electric potential energy gained by that:
W = V q and Ep = V q
Potential Difference | Kinetic Energy gained by a charged particle
The difference in Electric potential between a location in the electric field and another new location that the electron might move to is called the Potential Difference.
The Kinetic Energy gain by a charged particle: The potential difference for a device in an electrical circuit is defined as the energy transferred per coulomb of charge passing through the device. In an electric field, we can follow the same idea to determine how much kinetic energy a charged particle will gain by moving through a potential difference of V within the field.
This Kinetic energy gain is given by the equation Ek = Vq
Summary
Electric field concepts, definition, direction, and unit are what we discussed in this post. We also discussed the Electric field force and acceleration formula. Definition and formula of Electric Potential are also covered.
If you find it useful please share this using the share buttons on this page and bookmark our site as well.
Suggested Study:
Triboelectric charging
