Derive the Formula of Electric Potential Difference from the energy difference in an electric field
Last updated on February 4th, 2022 at 06:43 am
In this post, we will see how to derive the Formula of Electric Potential Difference from the concept of energy difference in an electric field. We will derive 2 equations of Electric Potential Difference.
In the example below a sample, positive charge +q is moved from position A to position B in an electric field E as shown in figure 1. d is the distance between A and B.
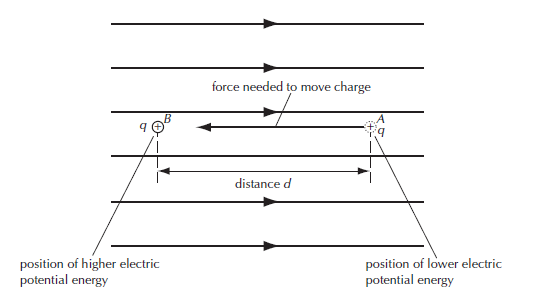
In this case, as the sample charge is a positive charge and the direction of the electric field is from the side of B to the side of A, that means this sample charge will be repelled. Hence, to move it towards B, work needs to be done. This results in an increase in electric potential energy and the sample charge gains this electrical energy.
Since the field is uniform, the force is constant. This makes it is very easy to calculate the work done(W) to move the sample charge in an electric field.
Work done = W = Force x displacement = F d = Eq d
Hence, the actual energy difference between A and B = Eq d
Also, the Potential energy gained here by the charge also equals Eq d.
In this example, the actual energy difference between A and B depended on the charge that was moved. If we doubled the charge we would double the energy difference.
The quantity that remains fixed between A and B is the energy difference per unit charge. This is called the potential difference, or p.d., between the points.
In other words, the potential difference between the two points is the work done in moving a unit positive charge from one point to another point.
Derive the Formulas of Electric Potential Difference
The potential difference or p.d. between 2 points= V= energy difference per unit charge moved = work done per unit charge moved = total work done / total charge moved = W/q
V = W/q ……………. (1) [equation of potential difference (pd) in terms of work done]
Again, we can write equation (1) a bit differently,
V = W/q = F d /q = Eq d/q = Ed
V = E d ……………. (2)
The basic unit for the potential difference is the joule/coulomb, J C–1.
A very important point to note is that for a given electric field, the potential difference between any two points is a single fixed scalar quantity.
The work done between these two points does not depend on the path taken by the test charge. A technical way of saying this is ‘the electric field is conservative’.
Unit: The SI unit of potential and the potential difference is volt (named after an Italian physicist Alessandro Volta) and is denoted by the symbol V.
From equation (1) above, 1 Volt = 1 Joule / 1 Coulomb
=> 1 V = 1 J C–1
Thus, the potential difference between two points is one volt if one Joule of work is done in moving one Coulomb charge from one point to the other.
The potential difference is measured by an instrument called Voltmeter. It is always connected in parallel to the electric element or the two points across which potential difference is to be measured.
