Electric Field due to a Point Charge – derivation of the formula

Last updated on May 13th, 2022 at 04:53 am

Let us apply Gauss’ Law to calculate electric field due to a point charge.
Draw a spherical surface of radius r with a point charge at the center of the sphere, as shown in Fig. 1

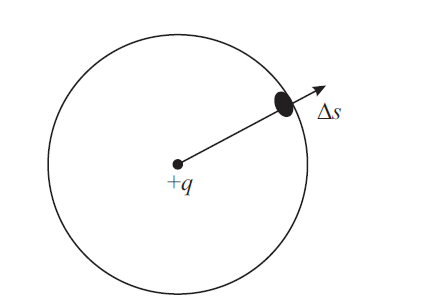
The electric field E is along the radial direction pointing away from the center and normal to the surface of the sphere at every point. The area vector is normal to the element of area Δs and is is parallel to E.

According to Gauss’ law, we can write

φ_E = _iΣ E_i.Δs_i = q/ε₀ ………………. (1)

[The electric flux Φ_E is defined as the scalar product of Area vector A and electric field E. Hence, Φ_E = E . A = EA cos θ
Here, the area vector is normal to the element of area Δs and is is parallel to E. Hence, θ = 0°. And, cos θ = cos 0° = 1. Hence, Φ_E = EA ]

E is same on all points on the surface, we can write
φ _E = EA = E x 4πr²

From equation (1) we can write:
E × 4πr² = q/ε₀

E = q/ (4π ε₀ r² )

=>E = [1/(4πε₀)] [q/r²] ………. (1) (Electric Field due to a Point Charge)

Coulomb Force derivation from Gauss’ Law

Using Gauss’ Law we have shown above that the Electric Field due to a Point Charge q can be expressed as:

E = q/ (4π ε₀ r² )

or, E = [1/(4π ε₀)] [q/r²]

If there is a second charge q₀ placed at a point on the surface of the sphere, the magnitude of the force on this charge would be

F = q₀ × E

so that, F = q q₀ / (4π ε₀ r² )

Do you recognize this result? It is the expression for Coulomb’s force between two static point charges.

Thus, Gauss’ law helps us to derive the Coulomb force equation.