Torque on an electric dipole – revision notes with definition, & equation (derivation)
Last updated on March 24th, 2022 at 04:27 pm
Here, we will study the concepts and formula of the torque on an electric dipole.
Torque on an electric dipole – how is it generated?
Two equal and opposite charges (q) each, separated by a small distance (2l) constitute an electric dipole (figure 1). When this dipole is placed in an electric field E then this results in two forces [qE and (–qE)] that are equal, opposite, and parallel, separated by a distance. These equal, opposite, and parallel forces constitute a couple. This couple generates torque on the electric dipole.
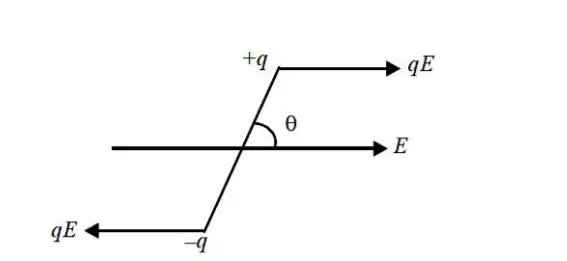
Equation of Torque on an electric dipole
The Torque on an electric dipole is availed by cross multiplication of the dipole moment p and the Electric Field E.
Torque (τ) = p x E
=> τ = p E Sin θ ……………..(1)
Note: read one related post to Know more about the Dipole moment ]
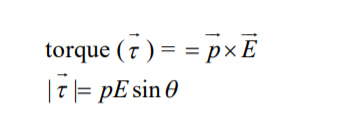
Direction of the torque on an electric dipole
This direction of the torque τ on an electric dipole is perpendicular to the plane containing dipole moment p and the electric field E.
The torque tends to align the dipole in the direction of the field.
When the dipole is parallel to the electric field, it is in stable equilibrium. When it is antiparallel to the electric field, it is in unstable equilibrium.
Maximum torque on an electric dipole
Torque is maximum when τ = 90°, i.e. when the dipole is perpendicular to E.
Therefore maximum torque on an electric dipole = pE, where p is the dipole moment and E is the electric field.
Derivation of the Equation of the Torque on an electric dipole
Let’s find out how to express Electric Force and Torque on an Electric Dipole in a Uniform Electric Field.
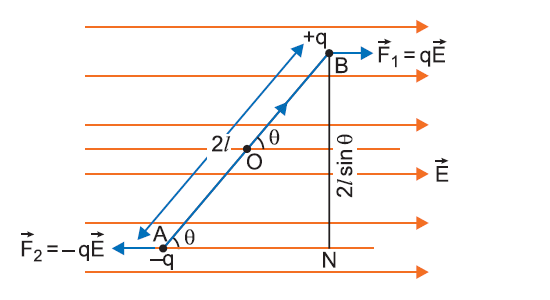
In a uniform electric field of strength E, the net electric force is zero; but torque will work on the dipole because of two equal and opposite forces acting on two charges at 2 ends of the dipole.
Torque τ = magnitude of a Force x perpendicular distance between the lines of 2 forces = qE 2l Sin θ = (q2l) E Sin θ = p E Sin θ = p x E
Hence, a torque equal to pE sin θ acts on the dipole (where θ is the angle between directions of dipole moment p and electric field E ).
This torque tends to align the dipole along the direction of the electric field. Torque in vector form:
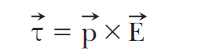
Summary:
Torque (τ) = p x E
=> τ = p E Sin θ
